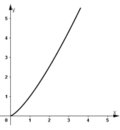
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = – 2x3 – 3x2 + 1; b) y = x3 + 3x2 + 3x + 2.
Những câu hỏi liên quan
Khảo sát sự biến thiên và vẽ đồ thị hàm số: y = x 3 + 3 x 2 + 1
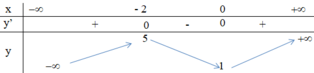
+ Bảng biến thiên:
Kết luận:
Hàm số đồng biến trên các khoảng (-∞; -2) và (0; +∞).
Hàm số nghịch biến trên khoảng (-2; 0).
Hàm số đạt cực tiểu tại x = 0 ; y C T = 1 .
Hàm số đạt cực đại tại x = -2 ; y C Đ = 5 .
- Đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (–3; 1), (1; 5).
Đúng 0
Bình luận (0)
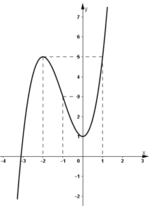
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: y = 1 2 x 4 - 3 x 2 + 3 2
Khảo sát hàm số y = 1 2 x 4 - 3 x 2 + 3 2
- TXĐ: D = R
- Sự biến thiên:
+ Chiều biến thiên:
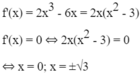
+ Giới hạn tại vô cực:
+ Bảng biến thiên:
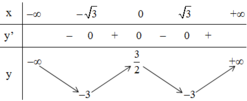
Hàm số đạt cực đại tại x = 0, yCĐ = 3 2
Hàm số đạt cực tiểu tại x =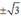 
; yCT = -3.
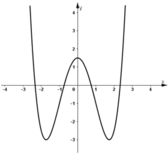
- Đồ thị:
+ Đồ thị hàm số nhận trục tung là trục đối xứng.
+ Đồ thị cắt trục tung tại (0; 1,5).
Đúng 0
Bình luận (0)
khảo sát sự biến thiên và vẽ đồ thị hàm số:
a. y=x3-3x2+2
b. y=x3+1
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
a) Khảo sát và vẽ đồ thị hàm số y=x3+3x2-4
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.
c) Chứng minh rằng điểm uốn làm tâm đối xứng của đồ thị.
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: f x = - x 3 + 3 x 2 + 9 x + 2
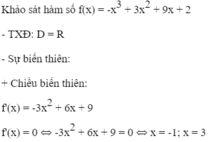
+ Giới hạn:
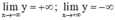
+ Bảng biến thiên:
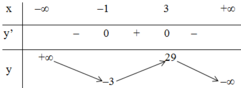
Kết luận:
Hàm số đồng biến trên (-1; 3)
Hàm số nghịch biến trên (-∞; -1) và (3; +∞).
Hàm số đạt cực đại tại x = 3, yCĐ = 29.
Hàm số đạt cực tiểu tại x = -1; y C T = - 3
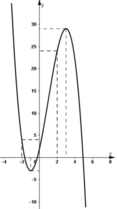
- Đồ thị:
+ Giao với trục tung tại (0; 2).
+ Đi qua các điểm (-2; 4); (2; 24).
Đúng 0
Bình luận (0)
a) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{x+2}\)
b) khảo sát và vẽ đồ thị hàm số \(y=\left|\dfrac{2x-3}{x+2}\right|\)
c) khảo sát và vẽ đồ thị hàm số \(y=\dfrac{2x-3}{\left|x+2\right|}\)
a) Khảo sát sự biến thiên và đồ thị (C) hàm số: f(x)=2x3+3x2+1
b) Tìm các giao điểm của đường cong (C) và parapol g(x) = 2x2+1 (P)
c) Viết Phương trình các tiếp điểm của (C) và (P) tại các điểm của chúng.
d) Xác định các khoảng trên đó (C) nằm phía trên và hoặc phía dưới (P).
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:a. yx3-3x+2b. yx3+1c. y -x3+3x+1d. y-x3-5x2-9x-4e. yx4-2x2-1f. y -dfrac{x^4}{2}-x2+dfrac{3}{2}g. y2x2-x4
Đọc tiếp
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a. y=x3-3x+2
b. y=x3+1
c. y= -x3+3x+1
d. y=-x3-5x2-9x-4
e. y=x4-2x2-1
f. y= \(-\dfrac{x^4}{2}\)-x2+\(\dfrac{3}{2}\)
g. y=2x2-x4
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số: y = x 4 3
Xét hàm số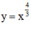 
ta có:
- Tập khảo sát : (0 ; +∞).
- Sự biến thiên:
+ 
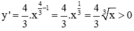với ∀ x > 0.
Do đó, hàm số đã cho đồng biến trên tập xác định.
+ Giới hạn:
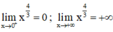
+ Tiệm cận : Đồ thị hàm số không có tiệm cận.
+ Bảng biến thiên:
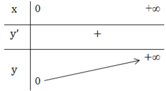
- Đồ thị hàm số:
Đúng 0
Bình luận (0)