chung minh các đường thẳng vuông góc kẻ từ một điểm của đường tròn ngoại tiếp một tam giác đến ba cạnh của một tam giác ấy nằm trên một đường thẳng

Những câu hỏi liên quan
Mỗi câu sau đây đúng hay sai?a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếpb) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếpc) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấyd) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.f) Giao điểm ba đường cao của một tam giác l...
Đọc tiếp
Mỗi câu sau đây đúng hay sai?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy.
e) Giao điểm ba đường phân giác trong của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy.
g) Tứ giác có tổng độ dài các cặp cạnh đối nhau bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn.
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó.
Câu a: Đúng Câu b: Sai Câu c: Sai
Câu d: Đúng Câu e: Đúng Câu f: Sai
Câu g: Đúng Câu h: Đúng Câu i: Sai
Đúng 0
Bình luận (0)
Mỗi câu sau đây đúng hay sai ?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn nội tiếp tam giác ấy
e) Giao điểm ba đường phân giác của một tam giác là tâm đường tròn nội tiếp tam giác ấy
f) Giao điểm ba đường cao của một tam giá...
Đọc tiếp
Mỗi câu sau đây đúng hay sai ?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn nội tiếp tam giác ấy
e) Giao điểm ba đường phân giác của một tam giác là tâm đường tròn nội tiếp tam giác ấy
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy
g) Tứ giác có tổng độ dài các cặp cạnh đối bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó
Các câu đúng : a, d, e, g, h
Các câu sai : b, c, f, i
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB với trung điểm O. trên một nửa mặt phẳng bờ AB kẻ các tia Ax By vuông góc với AB. trên AC lấy một điểm P bất kì từ O Kẻ OQ vuông góc với OP(Q thuộc By) Gọi P phải là giao điểm của các tia đối củaOP,By . tam giác OPP là tam giác gì... chứng minh đường thẳng PQ luôn tiếp xúc với đường tròn (O;OA)... chứng minh đường tròn ngoại tiếp tam giác OPQ luôn tiếp xúc với một đường thẳng cố định....
Đọc tiếp
Cho đoạn thẳng AB với trung điểm O. trên một nửa mặt phẳng bờ AB kẻ các tia Ax By vuông góc với AB. trên AC lấy một điểm P bất kì từ O Kẻ OQ vuông góc với OP(Q thuộc By) Gọi P' phải là giao điểm của các tia đối củaOP,By .
tam giác OPP' là tam giác gì..
. chứng minh đường thẳng PQ luôn tiếp xúc với đường tròn (O;OA).
.. chứng minh đường tròn ngoại tiếp tam giác OPQ luôn tiếp xúc với một đường thẳng cố định....
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.b, chứng minh: ∆ABD~∆MBCc, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố địn...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A đường thẳng vuông góc với AB cắt nửa đường tròn trên tại I . K là một điểm bàng kỳ nằm trên đoạn thẳng CI ( K khác C và I ), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D.
a, chứng minh : các tứ giác BCKM, ACMD nội tiếp đường tròn.
b, chứng minh: ∆ABD~∆MBC
c, chứng minh tâm đường tâm đường tròn ngoại tiếp tam giác ABC D nằm trên một đường thẳng tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định Khi K di động trên đoạn thẳn
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
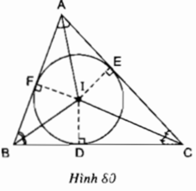
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.
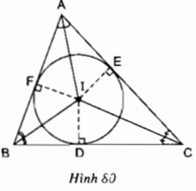
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
Đúng 0
Bình luận (0)
Từ một điểm P nằm trên đường tròn ngoại tiếp tam giác ABC, kẻ PD vuông góc với AB, PE vuông góc với BC, PF vuông góc với AC. Chứng minh 3 điểm D,E,F thẳng hàng
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Đọc tiếp
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Cho ba điểm A, B, C cố định nằm trên một đường thẳng và theo thứ tự đó. Đường tròn (O) thay đổi luôn đi qua B và C. Từ A kẻ các tiếp tuyến AM và AN với đường tròn (O) (M, N là hai tiếp điểm). Đường thẳng MN cắt AO tại H, gọi E là trung điểm của BC. Chứng minh rằng khi đường tròn (O) thay đổi, tâm của đường tròn ngoại tiếp tam giác OHE nằm trên một đường tròn cố định
Gọi I là giao điểm của MN và AC.
Ta có: \(\widehat{IHO}=\widehat{OEI}=90°\)
\(\Rightarrow\)Tứ giác EIHO nội tiếp đường tròn.
\(\Rightarrow\)Tâm của đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.(*)
Ta có ∆AIH \(\approx\)∆AOE
\(\Rightarrow\)AH.AO = AE.AI (1)
Ta có: ∆AMB \(\approx\)AOM
\(\Rightarrow\)AM2 = AH.AO (2)
Ta lại có: ∆ABM \(\approx\)∆AMC
\(\Rightarrow\)AM2 = AB.AC (3)
Từ (1), (2), (3) \(\Rightarrow\)AE.AI = AB.AC
Vì A,B,C,E cố định nên I cố định (**)
Từ (*), (**) suy ta tâm đường tròn ngoại tiếp ∆OHE nằm trên đường trung trực của EI.
PS: không chứng minh được nó nằm trên đường tròn nha b. Hình tự vẽ.
Đúng 0
Bình luận (0)
bạn cho mình hỏi tại sao tam giác ABM đồng dạng với tam giác AMC vậy?. Mình ko hiểu chỗ đó
Đúng 0
Bình luận (0)
Ta có:
\(\widehat{BAM}=\widehat{MAC}\)(là góc chung)
\(\widehat{BMA}=\widehat{ACM}\) (Do AM là tiếp tuyến tại M của (O) và 2 góc đó cùng chắn cung MB)
\(\Rightarrow\Delta ABM\approx\Delta AMC\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời












