Cho tam giác ABC vuông tại A có \(\frac{AB}{AC}=\frac{3}{4}\)và BC=15cm.Tính các độ dài AB,AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB/AC=3/4 và BC =15cm.Tính các độ dài AB,AC
Cho tam giác ABC vuông tại a có AB/AC=3/4 và BC=15cm.Tính độ dài AB,AC
Bài 1: Cho tam giác ABC cân tại B, kẻ CH vuông góc AB. Biết AH= 1cm, BH= 4cm. Tính độ dài AC.
Bài 2: Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
Bài 3: Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=BC.
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Đúng 0
Bình luận (0)
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=AC.
Cho tam giác ABC vuông tại A. Có \(\frac{AB}{AC}=\frac{3}{4}\)và đường cao AH (H thuộc BC). Tính độ dài các cạnh HB; HC
Cho tam giác ABC vuông tại A, BC=10cm, \(\frac{AB}{AC}=\frac{3}{4}\)
a) Tính độ dài các cạnh AB,AC
b) Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính độ dài đoạn thẳng MN,MC
Cho tam giác ABC vuông tại A, có BC=26 cm. Tính độ dài cạnh AB và AC biết rằng :\(\frac{AB}{AC}=\frac{5}{2}\)
lm ntn zạy các bn, help me
\(\frac{AB}{AC}=\frac{5}{2}=>AB=\frac{5}{2}AC\)
Áp dụng định lí Pi-ta-go vào tam giác ABC vuông tại A ta có :
\(AB^2+AC^2=BC^2\)
=> \(AB^2+AC^2=26^2(1)\)
Thay \(AB=\frac{5}{2}AC\)vào \((1)\)ta được :
\((\frac{5}{2}AC)^2+AC^2=26^2\Rightarrow\frac{25}{4}AC^2+AC^2=676\)
\(=>\frac{29}{4}AC^2=676=>AC^2\approx93,2=>AC\approx9,7\)
Đúng 0
Bình luận (0)
Bạn tự vẽ hình nha
\(\frac{AB}{AC}=\frac{5}{2}\Rightarrow\frac{AB}{5}=\frac{AC}{2}\).Đặt \(\frac{AB}{5}=\frac{AC}{2}=k\Rightarrow\hept{\begin{cases}AB=5k\\AC=2k\end{cases}}\)
Áp dụng định lí Pitago vào tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\)\(\Rightarrow\left(5k\right)^2+\left(2k\right)^2=26^2\)
\(\Rightarrow25k^2+4k^2=26^2\)\(\Rightarrow29k^2=676\)
\(\Rightarrow k^2=\frac{676}{29}\Rightarrow k=\frac{26}{\sqrt{29}}\)
\(\Rightarrow\hept{\begin{cases}AB=5.k=\frac{130}{\sqrt{29}}\\AC=2.k=\frac{52}{\sqrt{29}}\end{cases}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC \(\frac{AB}{AC}=\frac{3}{4}\)và AC - AB = 3. biết độ dài đường vuông góc kẻ từ A xuống BC là 7,2. Tính độ dài 2 hình chiếu của \(\frac{AB}{BC}\)và \(\frac{AC}{BC}\)
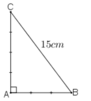
Cho tam giác ABC vuông tại A có AB/AC = 3/4 và BC = 15cm. Tính độ dài AB, AC
Theo đề bài ta có:
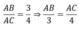
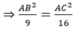
Theo tính chất dãy tỉ số bằng mhau ta có:
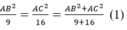
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
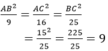
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)
Đúng 0
Bình luận (0)














