Cho A B tại A và B vẽ các cung tròn có các bán kính bằng nhau và lớn hơn một nửa AB .Hai cung tròn cắt nhau tại M và N. C/M MN là trung trực của AB
Những câu hỏi liên quan
Cho AB = 4cm. Vẽ cung tròn tâm A và B có bán kính bằng 3cm, cắt nhau tại M. Vẽ cung tròn tâm A và B có bán kính bằng 5cm, cắt nhau tại N. Chứng minh đường thẳng MN là trung trực của AB
Cho nửa đường tròn đường kính AB và dây MN có độ dài bằng bán kính (M thuộc cung AN, M khác A, N khác B). Các tia AM và BN cắt nhau tại I, các dây AN và BM cắt nhau tại K.
c. Tìm vị trí của dây MN để diện tích tam giác IAB lớn nhất
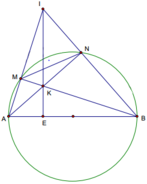
Chỉ ra sđ MN=60o nên tính được AIB=60o , do đó điểm I thuộc cung chứa góc 60o dựng trên đoạn AB.
Diện tích tam giác IAB lớn nhất khi IE lớn nhất (IE là đường cao của tam giác IAB), khi đó I nằm chính giữa cung chứa góc 60o dựng trên đoạn AB tương ứng với MN song song với AB.
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, gọi M là trung điểm của AB. Vẽ cung tròn tâm A và B có cùng bán kính ( bán kính lớn hơn MA ), hai cung tròn cắt nhau tại N.
a) Chứng minh tam giác NMA = tam giác NMB
b) Chứng minh NM vuông góc với AB
c) Biết rằng AB = 12cm; NM = 8 cm; NA = 10cm. Tính chu vi tam giác NMB
Xem chi tiết
a) Xét tam giác NMA và NMB có:
\(MA=MB\left(gt\right)\)
\(NM\) là cạnh chung.
\(NA=NB\) (đường tròn tâm A và B cùng bán kính cắt nhau)
\(\Rightarrow\Delta NMA=\Delta NMB\left(c.c.c\right)\) (1)
b) Vì \(\widehat{NMA}=\widehat{NMB}\) (từ 1) và 2 góc trên là 2 góc kề bù nên \(\widehat{NMA}=\widehat{NMB}=90^o\)
Vậy \(NM\perp AB\)
c) \(NA=NB\) (từ 1)
\(BM=\dfrac{AB}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Chu vi tam giác NMB:
\(10+8+6=24\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính AB và dây MN có độ dài bằng bán kính (M thuộc cung AN, M khác A, N khác B). Các tia AM và BN cắt nhau tại I, các dây AN và BM cắt nhau tại K.
a. Chứng minh rằng: IK vuông góc với AB
b. Chứng minh rằng:AK.AN+BK.BM=AB2
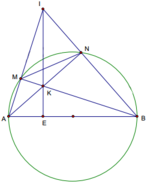
a. Ta thấy AN^ BI ,BM ^AI , nên K là trực tâm tam giác IAB. Do đó IK^ AB
b. Vì DAEK∽ DANB ∽ nên AK. AN =AE .AB
Tương tự vì DBEK∽ DBMA ∽ nên BK .BM =BE. BA
Vậy AK.AN+BK.BM=AE.AB+BE.BA=AB2
Đúng 0
Bình luận (0)
các bn giúp mình với:
Cho tam giác ABC sao cho AB=AC=3 cm. M là trung điểm của BC. Vẽ cung tròn tâm B(bán kính 3 cm) và cung tròn tâm C(bán kính 3cm) và 2 cung tròn cắt nhau tại D,E. Cho AM là tia phân giác của góc BAC. C/M M,A,D,E thẳng hàng.
Cho tam giác ABC sao cho AC=AB=3cm. Cho M là trung điểm của BC. Vẽ cung tròn tâm B và cung tròn tâm C đều có bán kính là 3cm và 2 cung tròn cắt nhau tại D,E. Chứng minh A,E,M,D thẳng hàng.
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:a) Tứ giác BCDE nội tiếp.b)góc AFE ACE.Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC cung CD cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:a) Các tam giác KAB và IBC là những tam giác đêu.b) Tứ giác KIBC nội tiếp.Bài 6. C...
Đọc tiếp
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE nội tiếp.
b)góc AFE= ACE.
Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:
a) Các tam giác KAB và IBC là những tam giác đêu.
b) Tứ giác KIBC nội tiếp.
Bài 6. Cho nửa đường tròn (0) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng:
a) Tứ giác FNEM nội tiêp.
b) Tứ giác CDFE nội tiếp.
Bài 7. Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC.
a) Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm 0 của đường tròn đó
b) Đường thẳng DH cắt đường tròn (0) tại điểm thứ hai là I. Chứng minh rằng năm điểm A, I, F, H, E cùng nằm trên một đường tròn
Các bạn giải giúp mình các bài này nhé, mình cảm ơn nhiều lắm
Bạn Long nêu cách dùng thước kẻ và compa vẽ đường thẳng đi qua một điểm A cho trước và vuông góc với một đường thẳng d cho trước như sau:- Vé cung tròn tâm A, bán kính chọn sao cho cung tròn ấy cắt d tại hai điểm B và C- Vẽ hai cung tròn tâm B và C có cùng bán kính sao cho chúng cắt nhau tại hai điểm M và N- Vẽ đường thẳng MNHáy vẽ hình và giải thích tại sao MN là đường thẳng đi qua A và vuông góc với d?
Đọc tiếp
Bạn Long nêu cách dùng thước kẻ và compa vẽ đường thẳng đi qua một điểm A cho trước và vuông góc với một đường thẳng d cho trước như sau:
- Vé cung tròn tâm A, bán kính chọn sao cho cung tròn ấy cắt d tại hai điểm B và C
- Vẽ hai cung tròn tâm B và C có cùng bán kính sao cho chúng cắt nhau tại hai điểm M và N
- Vẽ đường thẳng MN
Háy vẽ hình và giải thích tại sao MN là đường thẳng đi qua A và vuông góc với d?
cho nửa đường tròn (0;R)có đường kính AB .Vẽ bán kính OC vuông góc với AB.Trên cung BC lấy điểm M.Nối AM cắt OC ở E
a)chứng minh 4 điểm O,E,M,B cùng nằm trên một đường tròn
b)gọi H là trực tâm của tam giác OME chứng minh AOMH là hình thoi
c)các tia BM và OC cắt nhau ở F,các tia BE và AF cắt nhau tại K chứng minh H,K,M thẳng hàng