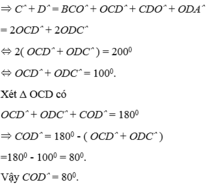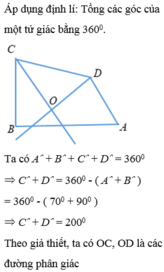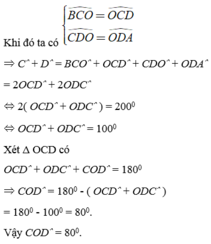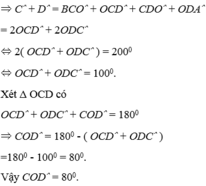cho tứ giác ABCD. tia phân giác góc B, D cắt nhau tại O. Chứng minh góc COD= A+B/2

Những câu hỏi liên quan
Cho tứ giác ABCD, phân giác các góc C và D cắt nhau tại O. Chứng minh : COD=A+B/2
Cho tứ giác ABCD. Phân giác góc C và góc D cắt nhau tại O . Chứng minh : góc COD = góc A + góc D chia 2
Cho tứ giác ABCD,phân giác các góc C và D cắt nhau tại O . Chứng minh : góc COD= góc A+góc B chia 2
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{C}+\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}\right)\)
\(\widehat{COD}=180^o-\frac{1}{2}\left(\widehat{C}+\widehat{D}\right)\)
\(=180^o-\frac{1}{2}\left[360^o-\left(\widehat{A}+\widehat{B}\right)\right]\)
\(=\frac{1}{2}\left(\widehat{A}+\widehat{B}\right)\)
lm hộ mk đi please ;(
1. Cho tứ giác ABCD có góc C - góc D 10o. Các tia phân giác góc A và B cắt nhau tại I. Biết góc AIB 65o. Tính góc C và D.
2. Cho tứ giác ABCD. Các tia phân giác góc A,B,C,D cắt nhau thành 1 tứ giác. Chứng minh tứ giác đó có tổng 2 góc đối 180o.
3. Tứ giác ABCD có góc A góc C 90o. Chứng minh phân giác góc B và D // với nhau hoặc trùng nhau.
Đọc tiếp
lm hộ mk đi please ;(
1. Cho tứ giác ABCD có góc C - góc D = 10o. Các tia phân giác góc A và B cắt nhau tại I. Biết góc AIB = 65o. Tính góc C và D.
2. Cho tứ giác ABCD. Các tia phân giác góc A,B,C,D cắt nhau thành 1 tứ giác. Chứng minh tứ giác đó có tổng 2 góc đối = 180o.
3. Tứ giác ABCD có góc A = góc C = 90o. Chứng minh phân giác góc B và D // với nhau hoặc trùng nhau.
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD phân giác góc C và D cắt nhau tại O.Chứng minh góc COD=góc A+B: 2
ta có A+B=360-(D+C)
<=> A+B=360-2(180-ODC-OCD)=360-360+2.COD=2COD
=>COD=(A+B)/2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD , phân giác góc C và D cắt nhau tại O . Chứng minh rằng :
\(\widehat{COD}=\frac{\widehat{A}+\widehat{B}}{2}\)
ta có A+B=360-(D+C)
<=> A+B=360-2(180-ODC-OCD)=360-360+2.COD=2COD
\(\Rightarrow\widehat{COD}=\frac{\widehat{A}+\widehat{B}}{2}\)
Đúng 0
Bình luận (0)
Xét \(\Delta COD\)có :
\(\widehat{COD}=180^o-\left(\widehat{C_1}+\widehat{D_1}\right)\)
\(=180^o-\frac{\widehat{C}+\widehat{D}}{2}\)
xÉT tứ giác ABCD có :
\(\widehat{C}+\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}\right)\)
Do đó : \(\widehat{COD}=180^o-\frac{360^o-\left(\widehat{A}+\widehat{B}\right)}{2}\)
\(\Rightarrow\widehat{COD}=\frac{\widehat{A}+\widehat{B}}{2}\)(đpcm)
Đúng 0
Bình luận (0)