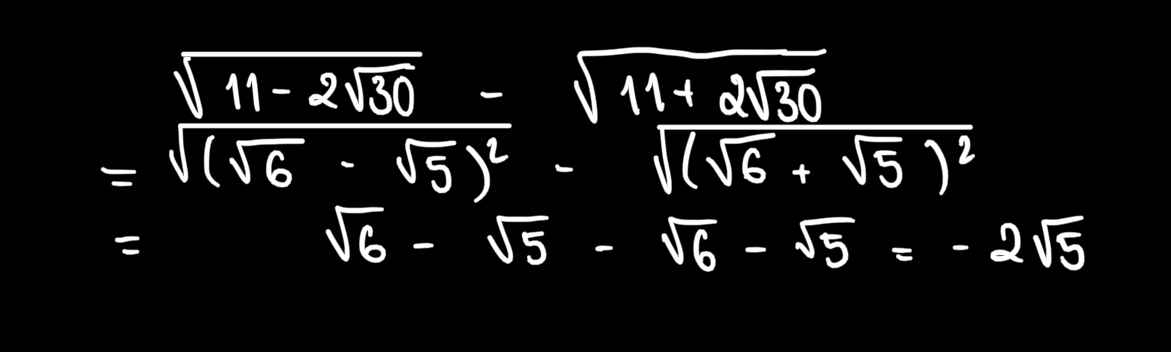\(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{\left(2\sqrt{2}+1\right)^2}}}\)

\(=\sqrt{13+30\sqrt{2+2\sqrt{2}+1}}=\sqrt{13+30\sqrt{\left(\sqrt{2}+1\right)^2}}\)

\(=\sqrt{13+30\left(\sqrt{2}+1\right)}=\sqrt{13+30\sqrt{2}+30}\)

\(=\sqrt{\left(5+3\sqrt{2}\right)^2}=5+3\sqrt{2}\)

#)Giải :

\(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+\sqrt{30\sqrt{2+\sqrt{8+2.2\sqrt{2+1}}}}}\)

\(=\sqrt{13+\sqrt{30\sqrt{2+\sqrt{\left(2\sqrt{2}+1\right)^2}}}}=\sqrt{13+\sqrt{30\sqrt{2+2\sqrt{2+1}}}}\)

\(=\sqrt{13+\sqrt{30\sqrt{\left(\sqrt{2}+1\right)^2}}}=\sqrt{13+\sqrt{30\left(\sqrt{2}+1\right)}}=\sqrt{13+\sqrt{30\sqrt{2}+30}}\)

Khó zậy

\(2\sqrt{3+\sqrt{5-\sqrt{13+4\sqrt{3}}}}=2\sqrt{3+\sqrt{5-\sqrt{12+4\sqrt{3}+1}}}\)

\(=2\sqrt{3+\sqrt{5-\sqrt{\left(2\sqrt{3}+1\right)^2}}}\)

\(=2\sqrt{3+\sqrt{5-2\sqrt{3}-1}}\)

\(=2\sqrt{3+\sqrt{3-2\sqrt{3}+1}}\)

\(=2\sqrt{3+\sqrt{3}-1}=2\sqrt{2+\sqrt{3}}\)

\(\sqrt{\frac{5+2\sqrt{6}}{5-2\sqrt{6}}}+\sqrt{\frac{5-2\sqrt{6}}{5+2\sqrt{6}}}=\sqrt{\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{\left(\sqrt{3}-\sqrt{2}\right)^2}}+\sqrt{\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{\left(\sqrt{3}+\sqrt{2}\right)^2}}\)

\(=\frac{\sqrt{2}+\sqrt{3}}{\sqrt{3}-\sqrt{2}}+\frac{\sqrt{3}-\sqrt{2}}{\sqrt{2}+\sqrt{3}}=\frac{\left(\sqrt{2}+\sqrt{3}\right)^2+\left(\sqrt{3}-\sqrt{2}\right)^2}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}=\frac{5+2\sqrt{6}+\left(5-2\sqrt{6}\right)}{3-2}=10\)

Sai de bai r ban Ngoc oi

Sai chỗ nào bạn Lâm ?

Ta có : \(\sqrt{2008+2\sqrt{2007}}=\sqrt{2007+2\sqrt{2007}+1}=\sqrt{\left(\sqrt{2007}+1\right)^2}=\sqrt{2007}+1\)

\(\sqrt{\left(1-\sqrt{2007}\right)^2}=\sqrt{2007}-1\)

Suy ra \(C=2\sqrt{2007}\)

Ta có  : \(x=\sqrt{\frac{5}{2}}+\sqrt{\frac{2}{5}}=\frac{5+2}{\sqrt{10}}=\frac{7}{\sqrt{10}}>0\)

Do đó : \(A=\sqrt{10x^2}-12x\sqrt{10}+36=x\sqrt{10}-12x\sqrt{10}+36=36-11x\sqrt{10}\)

\(=36-11.\sqrt{10}.\frac{7}{\sqrt{10}}=36-77=-41\)

Đề có sai ko bn , phải là 10x^2 ms khai triển hđt đc chứ

\(\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{5-\sqrt{5}}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)

\(=\left(\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)

\(=\left(\frac{-\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\frac{-\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.\)

\(=\left(\left(-\sqrt{7}\right)+\left(-\sqrt{5}\right)\right)\cdot\frac{\sqrt{7}-\sqrt{7}}{1}\)

\(=-\left(\sqrt{7}+\sqrt{5}\right)\cdot\frac{\sqrt{7}-\sqrt{5}}{1}\)

\(=\frac{-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}{1}\)

\(=\frac{-\left(7-5\right)}{1}=-2\)