Trên đường thẳng a cho 4 điểm M;N;P;Q xác định như sau:
MN = 12cm, điểm P thuộc đoạn thẳng MN sao cho NP = 5cm,điểm Q thuộc tia đối của tia MN = 2cm. Tính độ dài các đoạn MP,QN

Những câu hỏi liên quan
Cho điểm O nằm trên đường thẳng a.Vẽ tia Ox vuông góc với đường thẳng a.Trên Ox lấy điểm A sao cho OA=4 cm.Vẽ đường thẳng m là trung trực của OA,đường thẳng m cắt OA tại I.Tính OI,AI
bài 7: cho hai đường thẳng a, b phân biệt . Trên đường thẳng a lấy 21 điểm, trên đường thẳng b lấy 14 điểm ( không trùng với giao điểm nếu có ). Nối hai điểm bất kì trong 35n điểm ta được 1 đường thẳng. Hỏi có bao nhiêu đường thẳng được tạo thành?bài 8: cho 4 điểm A, B, C, D trong đó 3 điểm A, B, C thẳng hàng và 3 điểm A, B, D cũng thẳng hàng. Lấy điểm M không thuộc đường thẳng a. Vẽ các đường thẳng đi qua mỗi điểm. Hỏi mỗi diểm A, B, C, D, M là giao điểm của những đường thẳng nào? Giải thích rõ...
Đọc tiếp
bài 7: cho hai đường thẳng a, b phân biệt . Trên đường thẳng a lấy 21 điểm, trên đường thẳng b lấy 14 điểm ( không trùng với giao điểm nếu có ). Nối hai điểm bất kì trong 35n điểm ta được 1 đường thẳng. Hỏi có bao nhiêu đường thẳng được tạo thành?
bài 8: cho 4 điểm A, B, C, D trong đó 3 điểm A, B, C thẳng hàng và 3 điểm A, B, D cũng thẳng hàng. Lấy điểm M không thuộc đường thẳng a. Vẽ các đường thẳng đi qua mỗi điểm. Hỏi mỗi diểm A, B, C, D, M là giao điểm của những đường thẳng nào?
Giải thích rõ ràng
cho đường thẳng m lâý 2 điểm A và B nằm trên đường thẳng m . lấy điểm C không thuộc đường thẳng m . lấy điểm D nằm giữa A và B . kẻ các đường thẳng đi qua các cặp điểm trên a, trên hình vẽ có mấy đường thẳng phân biệt kể tên các đường thẳng đó b, trên hình vẽ ngững đường thẳng nào trùng nhauc, đường thẳng m cắt những đừng thẳng nào tìm giao điểm của đường thẳng m với các đường thẳng đó
Đọc tiếp
cho đường thẳng m lâý 2 điểm A và B nằm trên đường thẳng m . lấy điểm C không thuộc đường thẳng m . lấy điểm D nằm giữa A và B . kẻ các đường thẳng đi qua các cặp điểm trên
a, trên hình vẽ có mấy đường thẳng phân biệt kể tên các đường thẳng đó
b, trên hình vẽ ngững đường thẳng nào trùng nhau
c, đường thẳng m cắt những đừng thẳng nào tìm giao điểm của đường thẳng m với các đường thẳng đó
Trên đường thẳng Xy lấy điểm O và 2 điểm M và N sao cho OM=4 cm; ON=5 cm. Vẽ các điểm A và B trên đường thẳng Xy sao cho M là trung điểm của OB. Tính độ dài AB
Cho 4 điểm A,B,C,D. Trong đó 3 điểm A,B,C thẳng hàng và A,B,D thẳng hàng.
a, Chứng tỏ rằng 4 điểm A,B,C,D cùng nằm trên một đường thẳng.
b, M là một điểm không thuộc đường thẳng đi qua 4 điểm A,B,C,D.Vẽ đoạn thẳng AM,CM.Vẽ tia MB, vẽ đường thẳng DM.
a. Cho 4 điểm M N P Q trên đường thẳng xy
Đọc tên các tia,đoạn thẳng
b.Lấy 10 điểm khác trên đường thẳng xy.Khi đó có bn tia,bn đoạn thẳng
cho đường thẳng a và điểm A nằm ngoài đường thẳng a .B là điểm di chuyển trên đường thẳng a. trên tia đối của BA lay M sao cho BM=1/2BA.tìm quỹ tích điểm m
Lấy \(C\in a,C\ne B\), trên tia đối của tia \(CA\)lấy điểm \(N\)sao cho \(CN=\frac{1}{2}CA\).
Kẻ \(AK\perp MN,AK\)cắt \(BC\)tại \(H\).
Khi đó suy ra \(BC//MN\)
\(\frac{AK}{AH}=\frac{AM}{AB}=\frac{3}{2}\Rightarrow AK=\frac{3}{2}AH\).
Do đó điểm \(M\)luôn thuộc đường thẳng cố định (đường thẳng song song \(a\), khác phía với \(A\)cách \(a\)một khoảng \(\frac{1}{2}d\left(a,A\right)\).
Cho đường thẳng xy, lấy điểm O trên xy. Trên tia Ox lấy điểm A sao cho OA 2cm trên tia Oy lấy hai điểm M và B sao cho OM1 cm ,OB4 cm a) Chứng tỏ: Điểm M nằm giữa hai điểm O và B; Điểm M là trung điểm của đoạn thẳng ABb) Từ O kẻ hai tia Ot và Oz ,sao cho tOy130độ, zOy30độ.Tính số đotOzc) Trên mặt phẳng cho n đường thẳng trong đó bất kỳ hai đường thẳng nào cũng cắt nhau và không có ba đường thẳng nào cùng đi qua một điểm. Biết rằng tổng số giao điểm mà n đường thẳng đó cắt nhau tạo ra b...
Đọc tiếp
Cho đường thẳng xy, lấy điểm O trên xy. Trên tia Ox lấy điểm A sao cho OA =2cm trên tia Oy lấy hai điểm M và B sao cho OM=1 cm ,OB=4 cm
a) Chứng tỏ: Điểm M nằm giữa hai điểm O và B; Điểm M là trung điểm của đoạn thẳng AB
b) Từ O kẻ hai tia Ot và Oz ,sao cho tOy=130độ, zOy=30độ.Tính số đotOz
c) Trên mặt phẳng cho n đường thẳng trong đó bất kỳ hai đường thẳng nào cũng cắt nhau và không có ba đường thẳng nào cùng đi qua một điểm. Biết rằng tổng số giao điểm mà n đường thẳng đó cắt nhau tạo ra bằng 465. Tìm n
Hãy trình bày phương trình nhận biết các chất sau:a)3 lọ đựng 3 chất rắn mg;p2o5;Na b) 4 lọ đựng bốn chất khí Bao;K2o;Na;fe c) 4 lọ đựng bốn chất khí So2;N2;o2;h2
Đúng 0
Bình luận (1)
Dựa vào hình vẽ sau, nối mỗi ý ở cột A với một ý ở cột B để được kết quả đúng.
Cột A
Cột B
1. Điểm A
a) không thuộc các đường thẳng m, n, p, và q
2. Điểm B
b) nằm trên cả 3 đường thẳng m, n và p
3. Điểm C
c) nằm trên 2 đường thẳng m và n
4. Điểm D
d) nằm trên 2 đường thẳng m và q
e) nằm trên 2 đường thẳng p và q
A. 1_a; 2_b; 3_c; 4_d B. 1_b; 2_d; 3_e; 4_a C. 1_e; 2_b; 3_a; 4_d D. 1_a; 2_e; 3_c; 4_d
Đọc tiếp
Dựa vào hình vẽ sau, nối mỗi ý ở cột A với một ý ở cột B để được kết quả đúng.
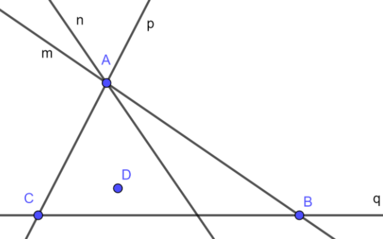
| Cột A | Cột B | |
| 1. Điểm A | a) không thuộc các đường thẳng m, n, p, và q | |
| 2. Điểm B | b) nằm trên cả 3 đường thẳng m, n và p | |
| 3. Điểm C | c) nằm trên 2 đường thẳng m và n | |
| 4. Điểm D | d) nằm trên 2 đường thẳng m và q | |
| e) nằm trên 2 đường thẳng p và q |
A. 1_a; 2_b; 3_c; 4_d
B. 1_b; 2_d; 3_e; 4_a
C. 1_e; 2_b; 3_a; 4_d
D. 1_a; 2_e; 3_c; 4_d
Đáp án là B
Điểm A thuộc 3 đường thẳng m, n và p ⇒ 1_b
Điểm B thuộc 2 đường thẳng m và q ⇒ 2_d
Điểm C thuộc hai đường thẳng p và q ⇒ 3_e
Điểm D không thuộc các đường thẳng m, n, p và q ⇒ 4_a
Đúng 0
Bình luận (0)
Trên đường thẳng a lấy 4 điểm E, F, G ,H nằm trên đường thẳng đó. Lấy điểm O∉a. Kể tên ba điểm không thẳng hàng. Hai đường thẳng d và d′ cắt nhau tại O. Lấy các điểm A, B, M, N trên đường thẳng d′ sao cho điểm O nằm giữa hai điểm A và B, điểm B nằm giữa hai điểm O và M, điểm N nằm giữa hai điểm O và A. Hỏi đường thẳng d có cắt các đoạn thẳng AB, AM và AN không? giúp mk nha, mk cảm ơn nhìu ạh
Đọc tiếp
Trên đường thẳng a lấy 4 điểm E, F, G ,H nằm trên đường thẳng đó. Lấy điểm O∉a. Kể tên ba điểm không thẳng hàng.
Hai đường thẳng d và d′ cắt nhau tại O. Lấy các điểm A, B, M, N trên đường thẳng d′ sao cho điểm O nằm giữa hai điểm A và B, điểm B nằm giữa hai điểm O và M, điểm N nằm giữa hai điểm O và A. Hỏi đường thẳng d có cắt các đoạn thẳng AB, AM và AN không?
giúp mk nha, mk cảm ơn nhìu ạh

Có 4 trường hợp 3 điểm thẳng hàng là: E,F,G; E,F,H; E,G,H; F,G,H.
Đúng 0
Bình luận (0)















