Cho đường tròn tâm O , đường kính AB các dây AC,AD . Gọi E là điểm bất kỳ trên đường tròn .H,K theo thứ tự là hình chiếu của E trên AC,AD . CMR : \(HB\le AB\)

Những câu hỏi liên quan
Cho đường tròn tâm O , đường kính AB các dây AC,AD . Gọi E là điểm bất kỳ trên đường tròn .H,K theo thứ tự là hình chiếu của E trên AC,AD . CMR : \(HB\le AB\)
Cho đường tròn tâm O , đường kính AB các dây AC,AD . Gọi E là điểm bất kỳ trên đường tròn .H,K theo thứ tự là hình chiếu của E trên AC,AD . CMR : \(HB\le AB\)
Cho đường tròn tâm O , đường kính AB các dây AC,AD . Gọi E là điểm bất kỳ trên đường tròn .H,K theo thứ tự là hình chiếu của E trên AC,AD . CMR : \(HB\le AB\)
Bài này khó lắm
mik mới chỉ lớp 7 thôi
làm sao đc bài này
mik ....
.....s...o...r.....r.......y
Đúng 0
Bình luận (0)
Bài này là bài 56 trang 98 của cuốn sách NÂNG CAO VÀ PHÁT TRIỂN TOÁN 9 TẬP 1 CỦA VŨ HỮU BÌNH nha.
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB, các dây AC, AD. Gọi E là điểm bất kì trên đường tròn, H và K theo thức wuj là hình chiếu của E trên AC, AD. Chứng minh HK $\le$ AB.
Kẻ đường cao AH, ta tính được AH = 32cm.
Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM AC.
Ta có: (g.g)
.
Từ đó tính được x = 7cm.
Các điểm A, H, E, K thuộc đường tròn có đường kính AE, mà HK là dây của đường tròn nên HK \le AE.
Trong đường tròn (O), ta có AE \le AB. Do đó HK \le AB.
Xem thêm câu trả lời
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:1) F là trung điểm của EH2) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.Giúp mình với, cảm ơn mn nhiều 3
Đọc tiếp
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:
1) F là trung điểm của EH
2) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.
Giúp mình với, cảm ơn mn nhiều <3
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:a) AC.HF AD.CFb) F là trung điểm của EHc) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.
Đọc tiếp
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn tâm O theo thứ tự tại C,D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng AD, AB, BD. Chứng minh rằng:
a) AC.HF = AD.CF
b) F là trung điểm của EH
c) Hai đường thẳng DC và DI đối xứng nhau qua đường thẳng DN.
Cho nửa đường tròn đường kính BC =2R, điểm A chuyển động trên nửa đường tròn đó. Gọi H là hình chiếu của A trên BC . Gọi D,E theo thứ tự là hình chiếu của H trên AC và AB . Gọi I,K lần lượt là trung điểm của HB và HC . Xác định vị trí của A để tứ giác DEIK có diện tích lớn nhất
Cho nửa đường tròn tâm O đường kính AB, dây CD có độ dài không đổi và khác AB. Gọi I là hình chiếu vuông góc của O trên CD; H,K theo thứ tự là hình chiếu vuông góc của A,B trên CD
a) Chứng minh I là trung điểm HK
b) Gọi E là hình chiếu vuông góc của I trên AB. Chứng minh rằng Sacb + Sadb = IE.AB
c) Tìm vị trí dây CD để diện tích AHKB lớn nhất
cứu mình với huuhhu
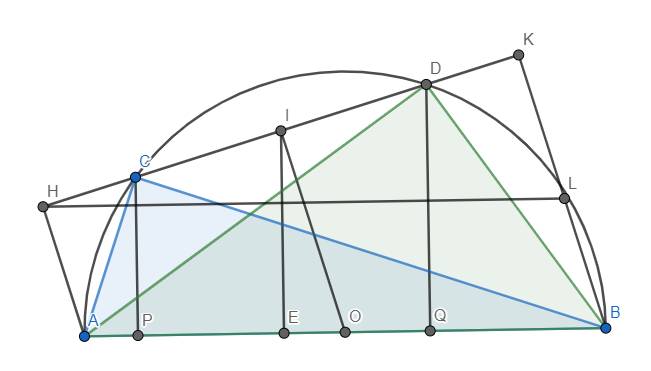
a) Ta thấy OI//AH//BK \(\left(\perp CD\right)\).
Xét hình thang ABKH (AH//BK), O là trung điểm AB. OI//AH \(\left(I\in HK\right)\) nên I là trung điểm HK.
b) Hạ \(CP\perp AB\) tại P, \(DQ\perp AB\) tại Q. Khi đó IE//CP//DQ \(\left(\perp AB\right)\).
Xét hình thang CDQP (CP//DQ) có I là trung điểm CD (hiển nhiên), IE//CP và \(E\in PQ\) nên IE là đường trung bình của hình thang CDQP \(\Rightarrow IE=\dfrac{CP+DQ}{2}\)
Lại có \(S_{ACB}=\dfrac{1}{2}AB.CP\), \(S_{ADB}=\dfrac{1}{2}.AB.DQ\)
\(\Rightarrow S_{ACB}+S_{ADB}=AB.\dfrac{CP+DQ}{2}=AB.IE\) (đpcm)
c) Ta có \(S_{AHKB}=\dfrac{AH+BK}{2}.HK=OI.HK\)
Do dây CD có độ dài không đổi nên khoảng cách từ O đến dây CD là OI cũng không đổi. Như vậy ta chỉ cần tìm vị trí của C để HK lớn nhất.
Thật vậy, dựng hình bình hành ABLH. Khi đó vì BK//AH nên \(L\in BK\). Đồng thời ta luôn có \(HK\le HL=AB\), suy ra \(S_{AHKB}\le OI.AB\).
Dấu "=" xảy ra \(\Leftrightarrow HK=HL\) \(\Leftrightarrow K\equiv L\) \(\Leftrightarrow\) AHKB là hình bình hành \(\Leftrightarrow\) HK//AB hay CD//AB \(\Rightarrow OI\perp AB\). Vậy C là điểm sao cho \(OI\perp AB\).
(Nếu muốn tìm cụ thể vị trí của C, thì mình nói luôn nó là điểm C sao cho \(sđ\stackrel\frown{AC}=180^o-2arc\cos\left(\dfrac{CD}{AB}\right)\) nhé. Chứng minh cái này dễ, mình nhường lại cho bạn.)
Đúng 2
Bình luận (0)
Chỗ vị trí C mình sửa lại là \(sđ\stackrel\frown{AC}=90^o-arc\sin\dfrac{CD}{AB}\) nhé.
Đúng 2
Bình luận (0)
a) Để chứng minh I là trung điểm HK, ta có thể sử dụng tính chất của tam giác vuông. Vì O là tâm của nửa đường tròn, nên IO vuông góc với CD. Tương tự, AI và BI cũng vuông góc với CD. Do đó, ta có tam giác IOA và tam giác IOB là tam giác vuông cân. Vì vậy, ta có AI = IB và IO = IO. Từ đó, ta có thể kết luận rằng I là trung điểm HK.
b) Để chứng minh rằng Sacb + Sadb = IE.AB, ta có thể sử dụng tính chất của tam giác vuông. Vì O là tâm của nửa đường tròn, nên IO vuông góc với CD. Tương tự, AI và BI cũng vuông góc với CD. Do đó, ta có tam giác IOA và tam giác IOB là tam giác vuông cân. Vì vậy, ta có AI = IB và IO = IO. Từ đó, ta có thể kết luận rằng Sacb + Sadb = IE.AB.
c) Để tìm vị trí dây CD để diện tích AHKB lớn nhất, ta cần xác định vị trí của I trên CD. Khi I là trung điểm HK, diện tích AHKB sẽ đạt giá trị lớn nhất
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho nửa đường tròn tâm O, đường kính AB. Gọi C là 1 điểm bất kì trên đường kính AB. Gọi C là 1 điểm bất kì trên đường tròn đó và M là điểm chính giữa của cung AC. Dây AC cắt dây BM tại H, dg thẳng AD cắt đg thẳng BC tại E
a)Chứng minh EMHC là tứ giác nội tiếp
b)EH vuông góc AB
c) Tam giác ABE cân
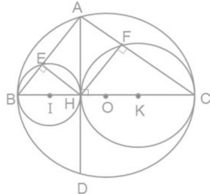
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Tứ giác AEHF là hình gì? Vì sao?
Cho đường tròn (O) có đường kính BC, dây AD vuông với BC tại H. Gọi E,F theo thứ tự là chân đường vuông góc kẻ từ H đến AB, AC. Gọi (I);(K) theo thứ tự các đường tròn ngoại tiếp tam giác HBE; HCF.
a) Hãy xác định vị chí tương đối của các đường tròn (I) ; (O) và (K).
b) Tứ giác AEHF là hình gì ? vì sao?
c) Chứng minh đẳng thức AE . AB= AF . AC