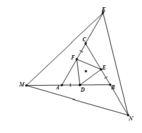
cho tam giác ABC đều .gọi EFD lần lượt thuộc các cạnh AB,BC,AC SAO CHO AD=CF=BE chứng minh DEF đều

Những câu hỏi liên quan
cho tam giác ABC đều .gọi EFD lần lượt thuộc các cạnh AB,BC,AC SAO CHO AD=CF=BE chứng minh BDF đều
cho tam giác ABC đều .gọi EFD lần lượt thuộc các cạnh AB,BC,AC SAO CHO AD=CF=BE chứng minh DEH đều
ABC đều. Gọi D,E,F là 3 điểm lần lượt nằm trên các cạnh AB, BC, CA sao cho AD=BE=CF a) Chứng minh rằng DEF là tam giác đều b) Gọi M, N, K là 3 điểm lần lượt nằm trên các tia đối của các tia AB, BC,CA sao cho AM=BN=CK Chứng minh là tam giác đều
Tam giác ABC đều. Gọi d,e,f là 3 điểm lần lượt nằm trên cạnh ab,bc,ca sao chi ad=be=cf a) chứng minh tam giác DEF là tam giác đều b) gọi m,n,k là 3 điểm làn lượt nằm trên các tia đối của các tia ab,bc,ca sao cho am=bn=ck. Chứng minh tam giác MNK là tam giác đều
vẽ hình giúp mình
Làm nhanh nhanh giúp mình nha!!!!😢😢
Cho tam giác ABC đều. Lấy các điểm D,E, F theo thứ tự thuộc các cạnh AB,BC,AC sao cho AD=BE=CF. Chứng minh rằng tam giác DEF đều.
Xét ΔABCΔABC là tam giác đều (gt)
=> {ABCˆ=ACBˆ=BACˆAB=AC=BC{ABC^=ACB^=BAC^AB=AC=BC (tính chất tam giác đều)
Có : ⎧⎩⎨⎪⎪D∈ABE∈BCF∈AC{D∈ABE∈BCF∈AC (gt)
=> ⎧⎩⎨⎪⎪AB=AD+BDAC=CF+CFBC=BE+CE{AB=AD+BDAC=CF+CFBC=BE+CE
Mà : {AD=BE=CFAB=AC=BC{AD=BE=CFAB=AC=BC (cmt)
=> BD=AF=CEBD=AF=CE
Xét ΔADF;ΔBEDΔADF;ΔBED có :
AF=BD(cmt)AF=BD(cmt)
DAFˆ=EBDˆDAF^=EBD^ (gt)
AD=BE(cmt)AD=BE(cmt)
=> ΔADF=ΔBED(c.g.c)ΔADF=ΔBED(c.g.c)
=> DF=DEDF=DE (2 cạnh tương ứng) (1)
Xét ΔADF;ΔCEFΔADF;ΔCEF có :
AF=EC(cmt)AF=EC(cmt)
DAFˆ=FCEˆDAF^=FCE^ (tam giác ABC đều - gt)
DA=FC(cmt)DA=FC(cmt)
=> ΔADF=ΔCEF(c.g.c)ΔADF=ΔCEF(c.g.c)
=> DF=EFDF=EF ( 2 cạnh tương ứng) (2)
- Từ (1) và (2) => DF=DE=EFDF=DE=EF
Xét ΔDEFΔDEF có :
DF=DE=EFDF=DE=EF (cmt)
=> ΔDEFΔDEF là tam giác đều (đpcm)
cho tam giác abc đều.Lấy điểm D,E,Ftheo thứ tự thuộc các cạnh AB,BC,AC sao cho : AD=BE=CF . Chứng minh : tam giác DEF đều
Cho tam giác đều ABC. Lấy các điểm D, E , F theo thứ tự thuộc các cạnh AB, BC và CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều?
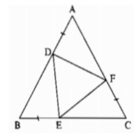
Ta có: AB = AD +DB (1)
BC = BE + EC (2)
AC = AF + FC (3)
AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)
AD = BE = CF ( giả thiết) (5)
Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF
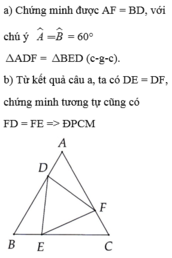
Xét ΔADF và ΔBED, ta có:
AD = BE (gt)
∠A =∠B =60o (vì tam giác ABC đều)
AF = BD (chứng minh trên)
suy ra: ΔADF= ΔBED (c.g.c)
⇒ DF=ED (hai cạnh tương ứng) (6)
Xét ΔADF và ΔCFE, ta có:
AD = CF (gt)
∠A =∠C =60o (vì tam giác ABC đều)
AF = CE (chứng minh trên)
suy ra: ΔADF= ΔCFE (c.g.c)
Nên: DF = FE (hai cạnh tương ứng) (7)
Từ (6) và (7) suy ra: DF = ED = FE
Vậy tam giác DFE đều
Đúng 1
Bình luận (0)
Cho tam giác ABC đều. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh:
a) tam giác ADF = tam giác BED.
b) tam giác DEF đều.
Cho tam giác đều ABC. Lấy các điểm D; E; F theo thứ tự thuộc các cạnh AB; BC; CA sao cho AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều.
\(\Delta ABC\)đều (gt) nên AB = BC = AC ; góc A = góc B = góc C = 600 mà AD = BE = CF (gt)
=> AB - AD = BC - BE = AC - CF <=> BD = CE = AF
\(\Delta ADF,\Delta BED\)có AD = BE (gt) ; góc DAF = góc EBD = 600 (cmt) ; AF = BD (cmt) nên\(\Delta ADF=\Delta BED\left(c.g.c\right)\)
=> DF = ED (2 cạnh tương ứng) (1)
\(\Delta ADF,\Delta CFE\)có AD = CF (gt) ; góc DAF = góc FCE = 600 (cmt) ; AF = CE (cmt) nên\(\Delta ADF=\Delta CFE\left(c.g.c\right)\)
=> DF = FE (2 cạnh tương ứng) (2).Từ (1) và (2),ta có DF = FE = ED.Vậy\(\Delta DEF\)đều
Đúng 2
Bình luận (0)
. Cho tam giác ABC, Các tia phân giác của các góc B và C cắt nhau tại I Qua I kẻ đường thẳng song song với BC cắt AB tại M và AC tại N. Chứng minh rằng MN = BM + CN