(4-2)^2-16=0

Những câu hỏi liên quan
a,(x^2-16)^2-16(x-4)^2=0
b, ( 2x/5-3/4)^2-(3x/5-1/4)^2=0
https://i.imgur.com/gxCqrM4.jpg
x=4x=4 là nghiệm của những phương trình nào dưới đây?
\frac{x^2-6x+8}{x^2-9x+20}=0x2−9x+20x2−6x+8=0 \frac{4x-16+\left(8-2x\right)}{x^2+16}=0x2+164x−16+(8−2x)=0 \frac{x^2-16}{x^3+16}=0x3+16x2−16=0 \frac{x^3-64}{x^2-16}=0x2−16x3−64=0Cho hỏi 1+2+3+4+...+1 0000...0 (16 chữ số 0)=? 1-2-3-4-...-1 0000...0 (16 chữ số 0)
1-2-3-4-...-1 0000...0 hơi sai sai. Số bé làm sao trừ được số lớn, lớp 5 cũng chưa học số âm?
Đúng 0
Bình luận (0)
giải hộ mk vs
1/2x^4+3x^3-x^2+3x+2=0
2/x^4-5x^3+7x^2-5x-16=0
3/(x+2)^4+(x+4)^4=16
1) \(2x^4+3x^3-x^2+3x+2=0\)
\(\Rightarrow2x^4+x^3+2x^3+x^2-2x^2-x+4x+2=0\)
\(\Rightarrow x^3\left(2x+1\right)+x^2\left(2x+1\right)-x\left(2x+1\right)+2\left(2x+1\right)=0\)
\(\Rightarrow\left(2x+1\right)\left(x^3+x^2-x+2\right)=0\)
\(\Rightarrow\left(2x+1\right)\left(x^3+2x^2-x^2-2x+x+2\right)=0\)
\(\Rightarrow\left(2x+1\right)\left[x^2\left(x+2\right)-x\left(x+2\right)+\left(x+2\right)\right]=0\)
\(\Rightarrow\left(2x+1\right)\left(x+2\right)\left(x^2-x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x+1=0\\x+2=0\\x^2-x+1=0\end{matrix}\right.\)
Ta có:
\(x^2-x+1\)
\(=x^2-2x.\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}+1\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Vì \(\left(x-\dfrac{1}{2}\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\) với mọi x
\(\Rightarrow x^2-x+1\) vô nghiệm
\(\Rightarrow\left[{}\begin{matrix}2x+1=0\\x+2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
3) \(\left(x+2\right)^4+\left(x+4\right)^4=16\)
Đặt x + 3 = a, ta được
\(\left(a-1\right)^4+\left(a+1\right)^4=16\)
\(\Rightarrow\left[\left(a-1\right)^2\right]^2+\left[\left(a+1\right)^2\right]^2=16\)
\(\Rightarrow\left(a^2-2a+1\right)^2+\left(a^2+2a+1\right)^2=16\)
\(\Rightarrow a^4+4a^2+1+2a^2-4a^3-4a+a^4+4a^2+1+2a^2+4a^3+4a=16\)
\(\Rightarrow2a^4+2.4a^2+2+2.2a^2=16\)
\(\Rightarrow2a^4+8a^2+4a^2+2=16\)
\(\Rightarrow2a^4+12a^2+2-16=0\)
\(\Rightarrow2a^4+12a^2-14=0\)
\(\Rightarrow2a^4-2a^2+14a^2-14=0\)
\(\Rightarrow2a^2\left(a^2-1\right)+14\left(a^2-1\right)=0\)
\(\Rightarrow\left(a^2-1\right)\left(2a^2+14\right)=0\)
\(\Rightarrow\left(a-1\right)\left(a+1\right).2\left(a^2+7\right)=0\)
\(\Rightarrow\left(a-1\right)\left(a+1\right)\left(a^2+7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a-1=0\\a+1=0\\a^2+7=0\end{matrix}\right.\)
Vì \(a^2\ge0\) với mọi a
\(\Rightarrow a^2+7\ge7\) với mọi a
\(\Rightarrow a^2+7\) vô nghiệm
\(\Rightarrow\left[{}\begin{matrix}a-1=0\\a+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+3-1=0\\x+3+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
a) 4(x^2-6x+9)-16(4x^2+28x+49)=0
b)(x2-16)^2-(x-4)^2=0
/ : căn bậc 2
Giúp với, cảm ơn.
a)(Sửa đề) \(4(x^2-6x+9)-16(4x^2+28x+49)=0\)
\(⇔(2x-6)^2-(8x+28)^2=0\)
\(⇔(-6x-34)(10x+22)=0\)
\(⇔\left[\begin{array}{} -6x-34=0\\ 10x+22=0 \end{array}\right.\)
\(⇔\left[\begin{array}{} x=-\dfrac{17}{3}\\ x=-\dfrac{11}{5} \end{array}\right.\)
b)(Sửa đề 1) \((2x-16)^2-(x-4)^2=0\)
\(⇔(3x-20)(x-12)=0\)
\(⇔\left[\begin{array}{} 3x-20=0\\ x-12=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=\frac{20}{3}\\ x=12 \end{array}\right.\)
(Sửa đề 2) \((x^2-16)^2-(x-4)^2=0\)
\(⇔(x^2-x-12)(x^2+x-20)=0\)
\(⇔(x-4)^2(x+3)(x+5)=0\)
\(⇔\left[\begin{array}{} (x-4)^2=0\\\ x+3=0\\ x+5=0 \end{array}\right.\)\(⇔\left[\begin{array}{} x=4\\\ x=-3\\ x=-5 \end{array}\right.\)
Bài 4 : Tính giá trị các biểu thức :
a. A= 22 - (-32)3 + 4-2 .16-2.52 .
b. B= (23 : 1/2) . 1/2+3-2.9-7. (14/25)0+5 .
c. C= 2-3 + (52)3.5-3+4-3 . 16 -2.32-105. (24/51)0 .
d. D= (2-3.1/2-2).2/3+4-2.8-7.(17/23)0+19 .
A=\(2^2-9^3+4^{-2}.16-2.5^2\)
\(=4-729+1-50=-774\)
B=\(\left(2^3.2\right).\dfrac{1}{2}+3^{-2}.3^2-7.1+5\)
\(B=2^4.\dfrac{1}{2}+1-7+5=8+1-7+5=7\)
Đúng 1
Bình luận (0)
C = 2-3 + (52)3.5-3 + 4-3.16 - 2.32 - 105.(\(\dfrac{24}{51}\))0
C = \(\dfrac{1}{8}\) + 56.5-3 + 4-3.42 - 2.9 - 105.1
C = \(\dfrac{1}{8}\) + 53 + \(\dfrac{1}{4}\) - 18 - 105
C = (\(\dfrac{1}{8}\) + \(\dfrac{1}{4}\)) - (105 - 125 + 18)
C = \(\dfrac{3}{8}\) - (-20 + 18)
C = \(\dfrac{3}{8}\) + 2
C = \(\dfrac{19}{8}\)
Đúng 0
Bình luận (0)
D = 2-3 . \(\dfrac{1}{2^{-2}}\).\(\dfrac{2}{3}\) + 4-2.8 - 7. (\(\dfrac{17}{23}\))0 + 19
D = 2-1.\(\dfrac{2}{3}\) + \(\dfrac{1}{16}\).8 - 7.1 + 19
D = \(\dfrac{1}{3}\) + \(\dfrac{1}{2}\) - 7 + 19
D = \(\dfrac{5}{6}\) + (19 - 7)
D = \(\dfrac{5}{6}\) + 12
D = \(\dfrac{77}{6}\)
Đúng 0
Bình luận (0)
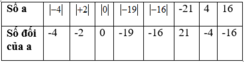
Tìm số đối của
−
4
;
+
2
;
0
;
−
19
;
−
16
;
−
21
;
4
;
16
Đọc tiếp
Tìm số đối của − 4 ; + 2 ; 0 ; − 19 ; − 16 ; − 21 ; 4 ; 16
A = {[(5^2 - 3) x 4 - 16 :2 + 6^0] : 3} + 25 - 16 : 2^3
a,(x-4).(x+3)=0
b,(x^2+16).(x^2-16)=0
c,(x^2+10).(x-3)<0
d,(-x^2-9).(2-x)<0
e,(x-2).(x+4)=0
Lam nhung cau cac ban biet nhe
Ai lam dung minh tick tick tick cho
a) \(\left(x-4\right)\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-4=0\\x+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-3\end{cases}}\)
Vậy \(x\in\left\{-3;4\right\}\)
b)\(\left(x^2+16\right)\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+16=0\\x^2-16=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{-16}\\x=\sqrt{16}=4\end{cases}}\)
Vậy \(x=4\)
Đúng 0
Bình luận (0)
\(\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-3\end{cases}}\)
\(\left(x^2+16\right)\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+16=0\\x^2-16=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=-16\left(loại\right)\\x^2=16\end{cases}}\Rightarrow x=\left(\pm4\right)^2\)
\(\left(x-2\right)\left(x+4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-4\end{cases}}\)
Đúng 0
Bình luận (0)
c) \(\left(x^2+10\right)\left(x-3\right)< 0\)
\(\Rightarrow\hept{\begin{cases}x^2+10\\x-3\end{cases}}\)trái dấu
TH1 : \(\hept{\begin{cases}x^2+10>0\\x-3< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2>-10\\x< 3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\inℤ\\x< 3\end{cases}}\Leftrightarrow x\in\left\{...;1;2\right\}\)
TH2 : \(\hept{\begin{cases}x^2+10< 0\\x-3>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2< -10\\x>3\end{cases}}\Leftrightarrow\hept{\begin{cases}x\in\varnothing\\x>3\end{cases}}\Leftrightarrow x\in\left\{\varnothing\right\}\)
\(\Rightarrow x\in\left\{...;1;2\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời