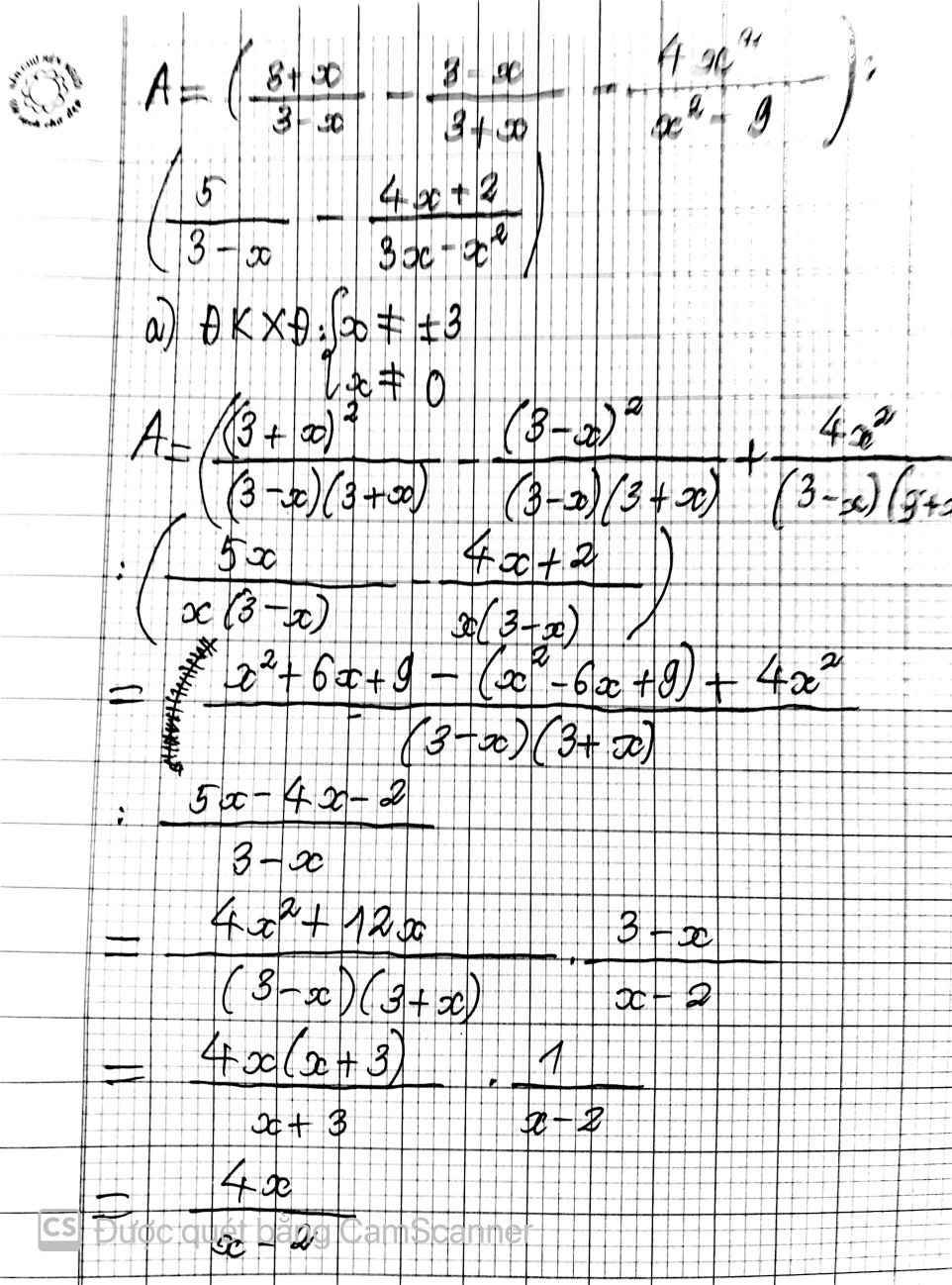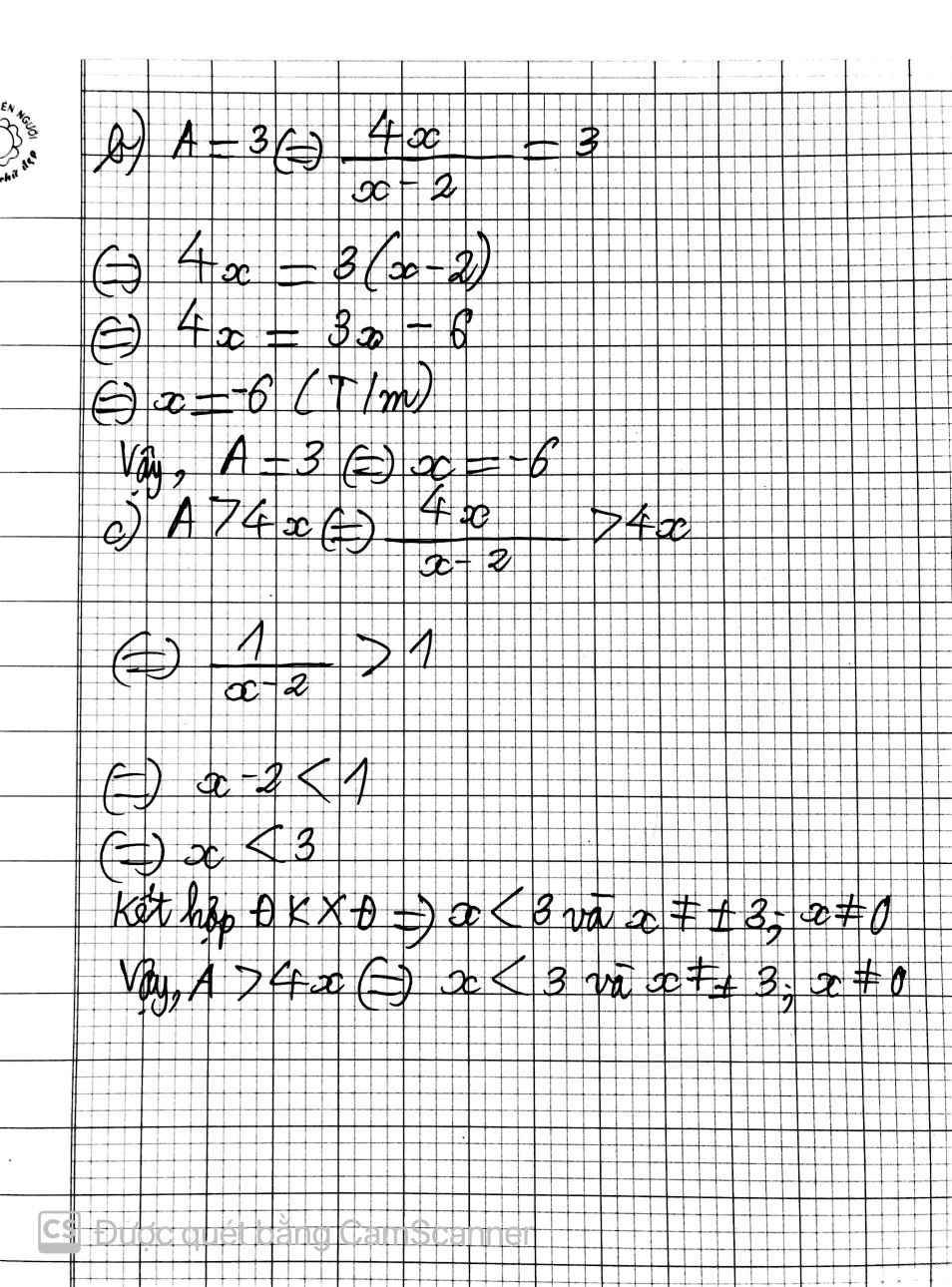Bai 3: Cho P = (x ^ 2 - 4x - 4)/(4 - x ^ 2) + (3x + 9)/(x + 2) a. Rút gọn P b.Tính giá trị P khi x = 8 c.Tìm x để P là số nguyên

Những câu hỏi liên quan
\(\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
a.Rút gọn biểu thức
b.Tính giá trị của P khi biết x=4+2\(\sqrt{3}\)
c.Tìm giá trị của Q để x=3
cho biểu thức A=(x+3/x-2+x+2/3-x+x+2/x^2-5x+6):(1-x/x+1)
a.rút gọn biểu thức A
b.tính giá trị của x,biết A>1
c.tìm tất cả các giá trị nguyên của x để biểu thức B=3.A nhận giá trị là một số nguyên
d Khi x>2,tìm giá trị nhỏ nhất của biểu thức C=A.x
a) \(\left(\frac{x+3}{x-2}+\frac{x+2}{3-x}+\frac{x+2}{x^2-5x+6}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{x+3}{x-2}-\frac{x+2}{x-3}+\frac{x+2}{x^2-2x-3x+6}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\frac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\right):\left(\frac{1-x}{x+1}\right)\)
= \(\left(\frac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}\right).\frac{x+1}{1-x}\)
=\(\frac{-3+x}{\left(x-2\right)\left(x-3\right)}.\frac{x+1}{1-x}\)
=\(\frac{1}{\left(x-2\right)}.\frac{x+1}{1-x}\)
=\(\frac{x+1}{\left(x-2\right)\left(1-x\right)}\)
b) Để A >1 \(\Leftrightarrow\frac{x+1}{\left(x-2\right)\left(1-x\right)}>1\)
\(\Leftrightarrow\frac{-\left(1-x\right)\left(3-x\right)}{\left(x-2\right)\left(1-x\right)}\)
\(\Leftrightarrow\frac{x-3}{x-2}>0\)
\(\Rightarrow\orbr{\begin{cases}x-3\ge0\\x-2>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge3\\x>2\end{cases}\Leftrightarrow}x\ge3}\)
\(\Rightarrow\orbr{\begin{cases}x-3< 0\\x-2< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 2\end{cases}\Leftrightarrow}x< 2}\)
Vậy ...
cho biểu thức A=(x+3/x-2+x+2/3-x+x+2/x^2-5x+6):(1-x/x+1)
a.rút gọn biểu thức A
b.tính giá trị của x,biết A>1
c.tìm tất cả các giá trị nguyên của x để biểu thức B=3.A nhận giá trị là một số nguyên
d Khi x>2,tìm giá trị nhỏ nhất của biểu thức C=A.x
Cho bt :
M=[x^2/(x^3-4x) + 6/(6-3x) + 1/(x+2) ] / [x-2+ (10-x^2)/(x+2)]a, Rút gọn bt
b,Tính giá trị của M khi x= -1/4
c, Tìm giá trị nguyên của x để giá trị của M nguyên
Cho A = ( x / x^2 - 16 - x - 4/ x^2 + 4x ) : 4x - 8 / x^2 + 4x + 8 / 4 - x
a, Rút gọn
b, Tìm giá trị nguyên của x để A có giá trị nguyên dương
giải chi tiết giùm nha
Cho biểu thức \(A=\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)
a, Tìm điều kiện của x để giá trị của phân thức xác định
b, Rút gọn biểu thức
c, Tính giá trị biểu thức khi x = 4
d, Tìm giá trị nguyên của x để A có giá trị là số nguyên.
a,ĐK: \(\hept{\begin{cases}x\ne0\\x\ne\pm3\end{cases}}\)
b, \(A=\left(\frac{9}{x\left(x-3\right)\left(x+3\right)}+\frac{1}{x+3}\right):\left(\frac{x-3}{x\left(x+3\right)}-\frac{x}{3\left(x+3\right)}\right)\)
\(=\frac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\frac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\frac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}.\frac{3x\left(x+3\right)}{-x^2+3x-9}=\frac{-3}{x-3}\)
c, Với x = 4 thỏa mãn ĐKXĐ thì
\(A=\frac{-3}{4-3}=-3\)
d, \(A\in Z\Rightarrow-3⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\Rightarrow x\in\left\{0;2;4;6\right\}\)
Mà \(x\ne0\Rightarrow x\in\left\{2;4;6\right\}\)
Đúng 1
Bình luận (0)
Bài 1: Cho A 4x^2/4-x^2 + 2+x/2-x - 2-x/2+x B x-3/2x-x^2a) Tính giá trị của B khi x 4b) Rút gọn Ac) Cho P A : B, tìm x để P 0 d) Tìm x để P -1e) Tìm x thuộc Z để A có giá trị nguyênf) Tìm GTNN của P khi x 3g) Đặt Q 4/P, so sánh Q và 1Bài 2: Cho A ( 3-x/x+3 . x^2+6x+9/x^2-9 + x/x+3 ) : 3x^2/x+3a) Rút gọn A b)Tính A, biết x^2-10c) Tìm x để A -1e) Tìm x để A x/8
Đọc tiếp
Bài 1: Cho A = 4x^2/4-x^2 + 2+x/2-x - 2-x/2+x
B = x-3/2x-x^2
a) Tính giá trị của B khi x = 4
b) Rút gọn A
c) Cho P = A : B, tìm x để P < 0
d) Tìm x để P = -1
e) Tìm x thuộc Z để A có giá trị nguyên
f) Tìm GTNN của P khi x > 3
g) Đặt Q = 4/P, so sánh Q và 1
Bài 2: Cho A = ( 3-x/x+3 . x^2+6x+9/x^2-9 + x/x+3 ) : 3x^2/x+3
a) Rút gọn A
b)Tính A, biết x^2-1=0
c) Tìm x để A < -1
e) Tìm x để A = x/8
Cho biểu thức
A = x/x+1 — x—3/9—x2 + 3x2—x—2/ x2+4x+3
a, Tìm ĐKXĐ và rút gọn A
b, Tìm các số nguyên x để A có giá trị là số nguyên
Cho biểu thức A=(3+x/3-x - 3 -x/3+x - 4x^2/x^2-9) : (5/3-x - 4x+2/3x-x^2) a. Rút gọn A b. Tìm x để A=3 c.tìm x để A>4x