
Những câu hỏi liên quan
1)Cho tam giác ABC(ABAC)có đường cao AH.Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CA,AB.a)C/m NP là đường trung trực của đoạn AHb)C/m tứ giác MNPH là hình thang cân.2)Cho tam giác ABC có chu vi 20cm.Gọi O là một điểm nằm trong tam giác;D,E,F lần lượt là trung điểm của OA;OB;OC.Tính chu vi tam giác DEF.3)Cho tam giác ABC có AM là trung tuyến.Gọi I là trung điểm của AM,gọi D là giao điểm của BI à AC.a)C/m AD1/2.DCb)So sánh độ dài BD và ID.
Đọc tiếp
1)Cho tam giác ABC(AB<AC)có đường cao AH.Gọi M,N,P lần lượt là trung điểm của các cạnh BC,CA,AB.
a)C/m NP là đường trung trực của đoạn AH
b)C/m tứ giác MNPH là hình thang cân.
2)Cho tam giác ABC có chu vi 20cm.Gọi O là một điểm nằm trong tam giác;D,E,F lần lượt là trung điểm của OA;OB;OC.Tính chu vi tam giác DEF.
3)Cho tam giác ABC có AM là trung tuyến.Gọi I là trung điểm của AM,gọi D là giao điểm của BI à AC.
a)C/m AD=1/2.DC
b)So sánh độ dài BD và ID.
1) Cho tam giác ABC có AB AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.a/ chứng minh PN là đường trung trực của AHb/ chứng minh tứ giác MNPH là hình thang2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB 60 độ. Gọi B , C lần lượt là hình chiếu của B, C trên AC và BD.a/ Chứng minh A, B, C 1/2 BCb/ gọi E là trung điểm BC, chứng minh tam giác EBC là tam giác đều
Đọc tiếp
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh A, B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
1) Cho tam giác ABC có AB AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.a/ chứng minh PN là đường trung trực của AHb/ chứng minh tứ giác MNPH là hình thang2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB 60 độ. Gọi B , C lần lượt là hình chiếu của B, C trên AC và BD.a/ Chứng minh B, C 1/2 BCb/ gọi E là trung điểm BC, chứng minh tam giác EBC là tam giác đều
Đọc tiếp
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
cho tam giác abc có góc a khác 90 độ , góc b và c nhọn , đường cao ah . vẽ các điểm d,e sao cho ab là trung trực của hd , ac là trung trực của he . gọi i và k lần lượt là giao điểm của de với ab . a) Chứng minh : Tam giác ADE cân tại A b)tính số đo góc aic và akb
A = 100* => B^ = C^ = 40*
trên CA lấy điểm E sao cho CB = CE
C^ = 40* và MCB^ = 20* => MCB^ = MCE^ = 20*
=> ΔCBM = Δ CEM ( c.g.c) => MEC^ = MBC^ = 10*
BCE^ = 40* và Δ BCE cân tại C => CEB^ = (180* - 40*)/2 = 70*
=>MEB^ = 60* (1)
ΔCBM = Δ CEM => MB = ME (2)
(1) và (2) => BME là tam giác đều MB = BE (1*)
ABC^ = 40* ; MBC^ = 10* => ABM^ = 30*
ABE^ = CBE^ - ABC^ = 70* - 40* = 30*
=> ABM^ = ABE^ (2*)
(1*) và (2*) => ΔABM = Δ ABE (vì có thêm AB là cạnh chung)
=> AMB^ = AEB^ = 70*
cho tam giác ABC vuông tại A (AB<AC). Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi S là giao điểm của AI và DE. a) Chứng minh tam giác IAB đồng dạng tam giác EAS. b)Gọi K là trung điểm AB, O là trung điểm BC. Chứng minh K, S, O thẳng hàng. c)Gọi giao điểm của KI và AC là M. Đường cao AH của tam giác ABC cắt DE tại N. Chứng minh AM=AN
cho tam giác ABC vuông tại A (AB<AC). Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi S là giao điểm của AI và DE. a) Chứng minh tam giác IAB đồng dạng tam giác EAS.
b)Gọi K là trung điểm AB, O là trung điểm BC. Chứng minh K, S, O thẳng hàng.
c)Gọi giao điểm của KI và AC là M. Đường cao AH của tam giác ABC cắt DE tại N. Chứng minh AM=AN
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH 12cm; BC 18cmBài 2: Cho tam giác ABC (AC AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:a, DE là đường trung trực của AHb, DEKH là hình thang cânBài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AHb, CM: AI vuôn...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
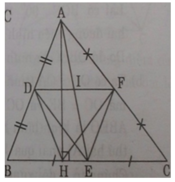
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC), AH là đường cao. Gọi D, E lần lượt là trung điểm của các cạnh AB và BC. Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và đường thẳng DE. Gọi N là giao điểm của CM và AH. Chứng minh rằng:
a) ΔABC đồng dạng ΔHBA
b) AH²=BH.CH
c) N là trung điểm của AH










