1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)

Vậy hpt có nghiệm (x;y) = (3;4)

2)

a) 3x² - 2x - 1 = 0

\(\Leftrightarrow3x^2-3x+x-1=0\)

\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)

Vậy pt có nghiệm x = 1 hoặc x = 3

b) Đặt x² = t (t \(\ge\) 0)

Pt trở thành: t² - 20t + 4 = 0

\(\Delta\) = (-20)² - 4.1.4 = 400 - 16 = 384

=> pt có 2 nghiệm phân biệt t₁ = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)

t₂ = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)

=> x₁ = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)

x₂ = \(2-\sqrt{6}\)

Cách 1 : Xác định các hệ số a, b, c.

a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2

⇒ tâm I (1; 1) và bán kính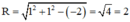 

b) 16x2 + 16y2 + 16x – 8y –11 = 0

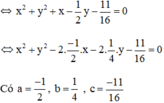
⇒ Đường tròn có tâm 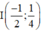 , bán kính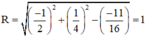 

c) x2 + y2 - 4x + 6y - 3 = 0

⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0

có hệ số a = 2, b = -3,c = -3

⇒ Đường tròn có tâm I(2 ; –3), bán kính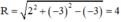 

Cách 2 : Đưa về phương trình chính tắc :

a) x2 + y2 - 2x - 2y - 2 = 0

⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4

⇔(x-1)2 + (y-1)2 = 4

Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.

b) 16x2 + 16y2 + 16x - 8y - 11 = 0

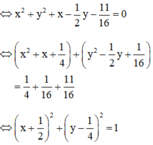
Vậy đường tròn có tâm 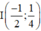 và bán kính R = 1.

c) x2 + y2 - 4x + 6y -3 = 0

⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3

⇔ (x - 2)2 + (y + 3)2 = 16

Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.

Ta có:  2 x + y 2 − 5 4 x 2 − y 2 + 6 4 x 2 − 4 x y + y 2 = 0          ( 1 ) 2 x + y + 1 2 x − y = 3       

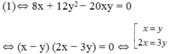
Với  x = y  ta có  2 ⇒ 3 x + 1 x = 3 ⇔ 3 x 2 - 3 x + 1 = 0 : phương trình vô nghiệm.

Với  2 x = 3 y  ta có  2 ⇒ 4 y + 1 2 y = 3 ⇔ 8 y 2 - 6 y + 1 = 0 ⇔ y = 1 2 y = 1 4

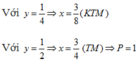
Đáp án cần chọn là: A

\(\left\{{}\begin{matrix}4x^2-4xy+y^2=9\\x+3y=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-y\right)^2=9\\x+3y=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x-y=3\\x+3y=5\end{matrix}\right.\\\left\{{}\begin{matrix}2x-y=-3\\x+3y=5\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-\frac{4}{7}\\y=\frac{13}{7}\end{matrix}\right.\end{matrix}\right.\)

Đáp án B

Ta có:

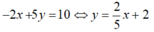
Nên tập nghiệm của phương trình – 2x + 5y = 10 được biểu diễn bởi đường thẳng ( d 1 ):

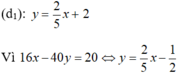
Nên tập nghiệm của phương trình 16x – 40y = 20 được biểu diễn bởi đường thẳng ( d 2 ):

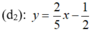
Hai đường thẳng  d 1 ;  d 2  có cùng hệ số góc và có tung độ góc khác nhau nên  d 1 //  d 2 .

Suy ra, hệ phương trình đã cho vô nghiệm.