Cho tam giác ABC đều, O nằm trong tam giác đó. CMR: 3 đoạn OA, OB, OC là độ dài 3 cạnh của tam giác

Những câu hỏi liên quan
Cho tam giác ABC đều, O bất kì nằm trong tam giác ABC. CMR: OA; OB; OC là độ dài 3 cạnh của một tam giác
- Chỉ cần nói cách vẽ thêm đường
Cho tam giác ABC đều . O nawmgf trong tam giác đó . CMR 3 đoan thẳng OA , OB, OC thỏa mãn BĐT tam giác
Cho tam giác đều ABC. O nằm bất kì trong tam giác ABC.CMR 3 đoạn OA,OB,OC đều thỏa mãn bất đẳng thức tong tam giác
3 đoạn thẳng OA,OB,OC thỏa mãn bất đẳng thức ta chứng minh
OA + OB > OC và OA - OB<OC .....
Trong tam giác AOB có OA + OB > AB => OA + OB > AC (1).
Do O nằm trong tam giác ABC => góc OAC < góc BAC => góc OAC < 60 độ
và góc OCA < góc BCA => góc OCA < 60 độ => góc AOC > 60 độ
trong tam giác AOC góc AOC lớn nhất => AC lớn nhất =>OC < AC (2)
từ (1) và (2) => OA + OB > OC tương tự ta có OB + OC > OA
=> OC > OA - OB hay OA-OB<OC....
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC biết AB=BC=AC. Giả sử O nằm trong tam giác đó sao cho OA=OB=OC. CMR o là giao điểm của ti
cho O nằm trong tam giác đều ABC thỏa mãn OA=1; OB= \(\sqrt{3}\); OC=2. Tính góc AOB;BOC;COA và cạnh của tam giác ABC
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
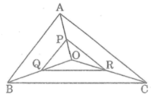
* Trong △ AOB ta có:
P trung điểm của OA (gt)
Q trung điếm của OB (gt)
Suy ra PQ là đường trung bình của △ AOB
Suy ra: PQ = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 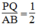 (1)
(1)
* Trong △ OAC, ta có:
P trung điểm của OA (gt)
R trung điểm của OC (gt)
Suy ra PR là đường trung bình của tam giác OAC.
Suy ra: PR =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 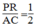 (2)
(2)
* Trong △ OBC, ta có:
Q trung điểm của OB (gt)
R trung điểm của OC (gt)
Suy ra QR là đường trung bình của tam giác OBC
Suy ra: QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 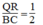 (3)
(3)
Từ (1), (2) và (3) suy ra: 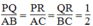
Vậy △ PQR đồng dạng △ ABC (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC đều,điểm O nằm trong tam giác .Trên cạnh AB',BC,CA lần lượt lấy D,E,F
a) C/m tứ giác ODBC là hình thang cân
b) C/m 3 đoạn OA,OB,OC thõa mãn bất đẳng thức tam giác.Giúp mình nhé!
Cho tam giác ABC O là một điểm bất kì nằm trong tam giác chứng minh rằng 3 đoạn thẳng OA,OB,OC thỏa mãn bất đẳng thức tam giác
Cho tam giác ABC có 3 cạnh bằng nhau. O là một điểm trong tam giác sao cho OA = OB = OC. Chứng minh rằng O là giao 3 tia phân giác các góc A, B, C của tam giác. (tức là OA là phân giác góc A, OB là phân giác góc B, OC là phân giác góc C)
Ta có AB=AC (GT), AO chung, OB=OC (GT) suy ra tam giác ABO=tam giác ACO (c.c.c)
suy ra góc BAO=góc CAO
mà O là điểm nằm trong tam giác ABC nên tia AO nằm giữa hai tia AB và AC
suy ra AO là tia phân giác của góc BAC (1)
chứng minh tương tự BO là tia phân giác của góc ABC (2)
CO là tia phân giác của góc ACB (3)
Từ(1), (2), (3) suy ra điều phải chứng minh















