Giải giúp mk bài này nhé :))) đề :
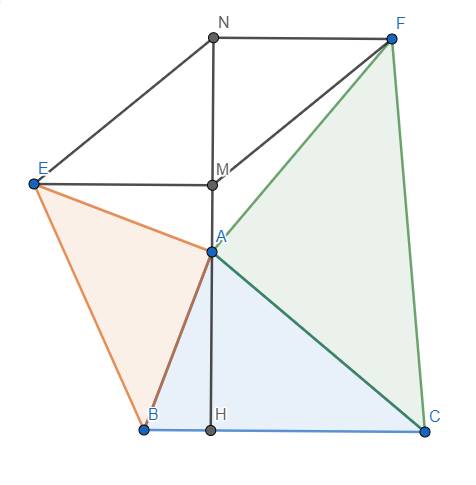
Cho tam giác ABC nhọn, vẽ AH vuông góc BC .Vẽ các tam giác vuông cân phía ngoài ABE, ACF nhận A làm đỉnh góc vuông. Kẻ EM, FN vuông góc AH .C/M
A/ TAM GIÁC AHB= TAM GIÁC EMA
B/ EM+BH =HM ;FN +CH =HN
C/ T LÀ TRUNG ĐIÊM CỦA EF