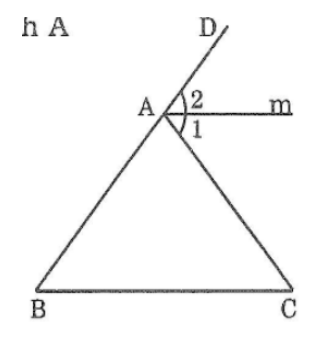
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=50^o\).Gọi Am là tia phân giác của góc ngoài ở đỉnh A.CMR Am//BC

Những câu hỏi liên quan
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=50^0\). Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am // BC ?
Cho hình trên
Ta có
CAz là góc ngoài của A nên
CAz=B+C=50*+50*=100* (theo định lý góc ngoài của một tam giác)
Am là phân giác của CAz nên
A1=A2=\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) 1/2 100*= 50*
=>A2=C (=50*)
Mà A2 và C là cặp góc so le trong nên
=> BC//Am (đpcm)
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (1)
Cho tam giác ABC có\(\widehat{B}=\widehat{C}=40^o\).Gọi Ax là tia phân giác của góc ngoài của đỉnh A.CMR Ax//BC
Cho tam giác ABC có góc B = C=50 độ. Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng minh rằng Am// BC
cho tam giác ABC có B=C=50 độ gọi ax là tia đối của ABAM là
tia phân giác của xÁc
tính góc xac
chứng minh Am song song vs BC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có B = C = 50 độ. Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am//BC
Cho tam giác ABC có góc B = góc C = 500. Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am//BC.
ta có góc BAC+B+C=180 độ=> BAC=180-50-50=80 độ
ta có góc IAB=180 độ-BAC=180-80=100 độ (IAB là góc ngoài ở đỉnh A)
mà Am la pg=> IAm=mAB=IAB:2=100:2=50 độ
ta có góc IAm= góc C=50 độ ,2 góc này ở vị trí đồng vị
=> Am// BC
Đúng 0
Bình luận (0)
ta có hình vẽ:
Theo tính chất góc ngoài của tam giác , ta có: góc CAn = góc B +góc C= 50+50=100 độ
=> góc CAm= góc CAn : 2= 100 độ :2 = 50 độ
=> Am // BC ( so le trong)
Đúng 0
Bình luận (0)
Cho tam giác ABC có <B=50 độ; <C=50 độ. GỌI Am là tia phân giác của góc ngoài đỉnh A của tam giác ABC. Chứng minh: Am//Bc
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A
⇒∠(CAD ) =∠B +∠C =50o+50o=100o
(tính chất góc ngoài tam giác)
∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50o (vì tia Am là tia phân giác của ∠(CAD)
Suy ra: ∠(A1) =∠C =50o
⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
Cho tam giác ABC có góc B = góc C = 50 độ . Gọi Am là tia phân giác của góc ngoài ở đỉnh A . Chứng minh Am // BC
Giúp Chi với
Gọi góc ngoài đỉnh A chứa tia phân giác Am là \(\widehat{xAB}\)
Xét tam giác ABC có \(\widehat{xAB}\) là góc ngoài => \(\widehat{xAB}=\widehat{ABC}+\widehat{ACB}=50^0+50^0\)\(=100^0\)
Vì Am là tia phân giác \(\widehat{xAB}\)=> \(\widehat{xAm}=\widehat{mAB}=\frac{\widehat{xAB}}{2}=\frac{100^0}{2}=50^0\)
Ta thấy \(\widehat{mAB}=\widehat{ABC}\left(=50^0\right)\)mà chúng là 2 góc so le trong
=> Am // BC (đpcm)
xét tam giác ABM và tam giác ACM có:
A1=A2 (GIẢ THUYẾT)
AM:cạnh chung
GÓC B=GÓC C(=50\(^O\))
DO đó tam giác ABM = tam giác ACM(G.C.G)
Tự vẽ hình
Ta vẽ góc ngoài ở đỉnh A. Đặt góc ngoài là góc TAC
Vì góc TAC là góc ngoài của tam giác ABC nên
=> TAC=ABC+ACB
mà ABC=ACB => ABC=ACB=TAC/2 (1)
Và AM là tia phân giác nên
=> TAM= MAC = TAC/2 (2)
Từ (1) và (2) => MAC=ACB
mà 2 góc này ở vị trí so le trong nên
=> AM//BC ( đpcm)
Xem thêm câu trả lời
Cho tam giác ABC có \(\widehat{B}=\widehat{C=40}^o\) Gọi Ax là tia phân giác của góc ngoài đỉnh A. chứng minh rằng Ax//BC
Cho tam giác ABC có \(\widehat{B}=\widehat{C}=40^0\). Gọi Ax là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ Ax // BC ?
Giải
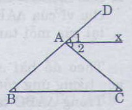
= + (góc ngoài của tam giác ABC)
= 400+ 400 = 800
400.
Hai góc so le trong bằng nhau nên Ax// Bc
Đúng 0
Bình luận (0)