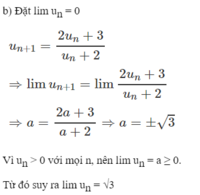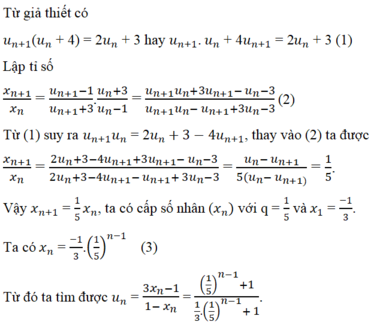(Un) với U1=4 Un+1= (Un^2-Un+9)/5 Chứng minh (Un) tăng

Những câu hỏi liên quan
Cho dãy số
u
n
, biết
u
1
-
1
,
u
n
+
1
u
n
+
3
v
ớ
i
n
≥...
Đọc tiếp
Cho dãy số u n , biết u 1 = - 1 , u n + 1 = u n + 3 v ớ i n ≥ 1 .
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: u n = 3 n – 4
a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.
Đúng 0
Bình luận (0)
cho dãy số un xác định bởi u1 = 2021
un+1= (un^2021 - un + 16)/(un^2020 - un + 17)
a) chứng minh un không tồn tại giới hạn hữu hạn
b) đặt Sn = Σ 1/(un^2020 + 3) tính lim Sn
Cho dãy số
(
u
n
)
u
1
1
;
u
2
...
Đọc tiếp
Cho dãy số ( u n ) u 1 = 1 ; u 2 = 2 u n + 1 = 2 u n - u n - 1 + 1 v ớ i n ≥ 2
a) Viết năm số hạng đầu của dãy số;
b) Lập dãy số ( v n ) với v n = u n + 1 − u n . Chứng minh dãy số (vn) là cấp số cộng;
Cho U1=2015,Un+1=Un/Un+2 tính U21 b)U1=2015;Un+1=2Un+5.Tính A= U10+5U12+U20/U5
Cho dãy số (Un) xác định như sau : U1=1; U2=5, Un+2 = 2*(Un+1)^2 - Un (nếu n lẻ) và Un+2 = Un+1 - 2*(Un)^2 (nếu n chẵn). n>=1. Tính U13 + U14
Cho dãy số
(
u
n
)
xác định bởi
u
1
1
u
n
+
1...
Đọc tiếp
Cho dãy số ( u n ) xác định bởi u 1 = 1 u n + 1 = 2 u n + 3 u n + 2 v ớ i n ≥ 1
a) Chứng minh rằng u n > 0 với mọi n.
b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
Cho dãy số
(
u
n
)
:
u
1
0
u
n
+
1
...
Đọc tiếp
Cho dãy số ( u n ) : u 1 = 0 u n + 1 = 2 u n + 3 u n + 4 v ớ i n ≥ 1
a) Lập dãy số ( x n ) với x n = u n - 1 u n + 3 . Chứng minh dãy số là cấp số nhân.
b) Tìm công thức tính x n , u n theo n.
Cho (Un) với U1=1 Un+1= 2Un - 2 Tìm Un
Cho dãy (un) với u1=1
Un= 5u(n-1) -3 (n>=2) lập dãy với vn=un-18 . chứng minh (vn) là một cấp số nhân
\(u_n-18=5u_{n-1}-21=5\left(u_{n-1}-18\right)+69\)
Đặt \(v_n=u_n-18\Rightarrow\left\{{}\begin{matrix}v_1=-17\\v_n=5v_{n-1}+69\end{matrix}\right.\)
\(\Rightarrow v_n+\frac{69}{4}=5\left(v_{n-1}+\frac{69}{4}\right)\)
Đặt \(v_n+\frac{69}{4}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\frac{1}{4}\\x_n=5x_{n-1}\end{matrix}\right.\)
\(\Rightarrow x_n\) là CSN với công bội \(q=5\Rightarrow x_n=x_1.q^{n-1}=\frac{1}{4}5^{n-1}\)
\(\Rightarrow v_n=x_n-\frac{69}{4}=\frac{1}{4}5^{n-1}-\frac{69}{4}\)
Bạn coi lại đề bài, rõ ràng đây ko phải là 1 cấp số nhân