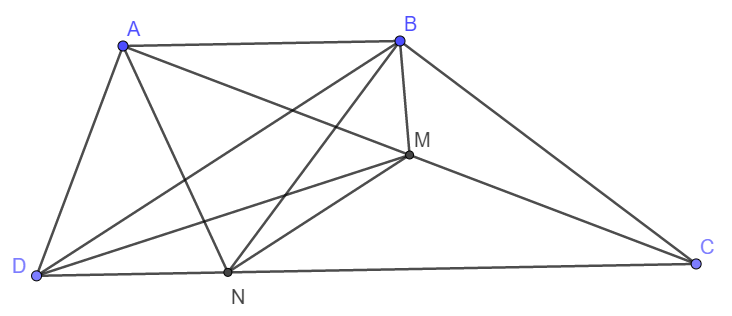
1.Cho hình thang ABCD có 2 đáy AB và CD . Điểm M nằm trên nằm trên đoạn thẳng AC sao cho AM = CM;điểm N trên cạnh CD sao cho MN song song với BD . Biết diện tích hình thang ABCD=16cm2.
a) CM : Diện tích hình tam giác BMN bằng diện tích hình tam giác DMN
b) Tính diện tích hình tứ giác ABND
2.Cho A=\(\frac{1}{1\times101}+\frac{1}{2\cdot102}+....+\frac{1}{25\cdot125}\)
B=\(\frac{1}{1\cdot26}+\frac{1}{2\cdot27}+....+\frac{1}{100\cdot125}\)
Tính \(\frac{A}{B}\)
Các bạn ơi giúp mk nhé !