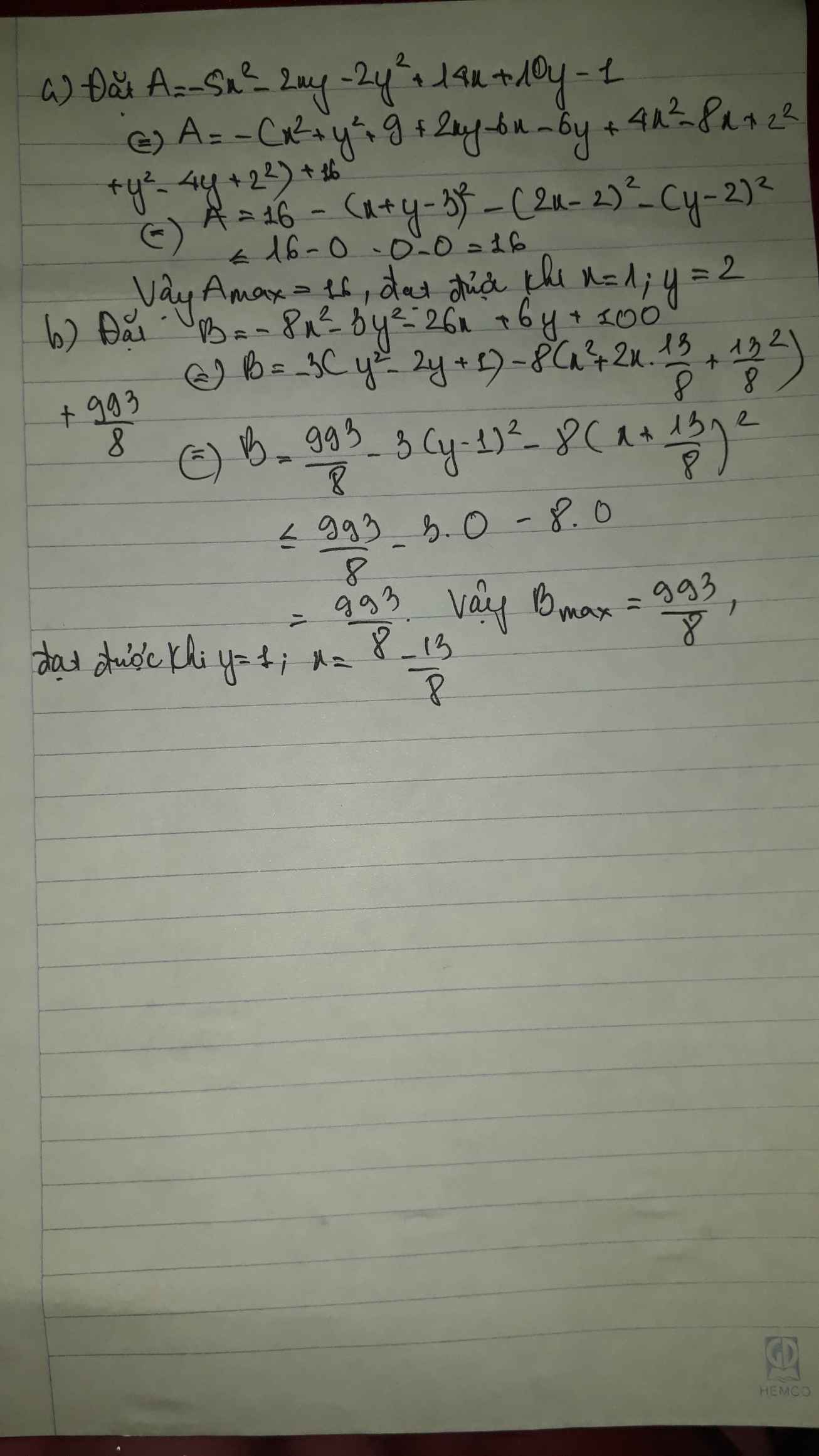\(E=-8x^2-3y^2-26x+6y+100\)

\(E=\left(-8x^2-26x\right)+\left(-3y^2+6y\right)+100\)

\(E=\left(-8x^2-13x-13x-169+169\right)+\left(-3y^2+3y+3y-9+9\right)+100\)

chết chết sr mình nhấn lộn đang định nhấn nút huỷ

E=-8(x^2+13x/4+169/64)-3(y^2-2y+1)+607/8

=-8(x+13/8)^2-3(y-1)^2+607/8

=> GTLN là 607/8

`Answer:`

\(P=8x^2+3y^2-8xy-6y+21\)

\(=\left(8x^2-8xy+2y^2\right)+y^2-6y+9+12\)

\(=2.\left(4x^2-4xy+y^2\right)+\left(y-3\right)^2+12\)

\(=2.\left(2x-y\right)^2+\left(y-3\right)^2+12\)

\(\Rightarrow P\ge2.0+0+12=12\)

Dấu "=" xảy ra khi \(\hept{\begin{cases}x=\frac{3}{2}\\y=3\end{cases}}\)

Ta có : 

\(P=8x^2+3y^2-8xy-6y+21\)

\(=\left(8x^2-8xy+2y^2\right)+\left(y^2-6y+9\right)+12\)

\(=2\left(4x^2-4xy+y^2\right)+\left(y-3\right)^2+12\)

\(=2\left(2x-y\right)^2+\left(y-3\right)^2+12\)

Ta có 

\(2\left(2x-y\right)^2+\left(y-3\right)^2\ge0\) với mọi x , y 

Suy ra : 

\(2\left(2x-y\right)^2+\left(y-3\right)^2+12\ge12\)

\(\Leftrightarrow P\ge12\)

 Dấu " = " xảy ra khi \(2x-y=y-3=0\) .  Suy ra  \(x=\frac{3}{2},y=3\)

Vậy GTNN của P là 12, đạt được khi \(x=\frac{3}{2},y=3\)

đề sai rồi bạn nhé