bạn ơi, cho mình xin cái dữ kiện về chiều dài được ko, cần thêm dữ kiện về 1 cạnh nào đó, chẳng hạn nó dài bao nhiêu

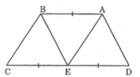
Vì CD = 2AB (gt) nên AB = 1/2 CD

Vì E là trung điểm của CD nên DE = EC = 1/2 CD

Suy ra: AB = DE = EC

Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau

Xét △ AEB và  △ CBE, ta có:

∠ (ABE) =  ∠ ( BEC)(So le trong)

∠ (AEB) =  ∠ (EBC) (so le trong)

BE cạnh chung

⇒ △ AEB = △ CBE (g.c.g) (1)

Hình thang ABCE có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau

Xét  △ AEB và  △ EAD, ta có:

∠ (BAE) =  ∠ (AED)(so le trong)

∠  (AEB) =  ∠ (EAD) (so le trong)

AE cạnh chung

⇒ △  AEB = △ EAD(g.c.g) (2)

Từ (1) và (2) suy ra: ΔAEB = ΔCBE = ΔEAD

Vậy ba tam giác  △ AEB;  △ CBE và  △ EAD đôi một đồng dạng

Trần Đăng Khang tham khảo nhé:

Tứ giác ABCD là hình thang nên:AB//CD. 
Gọi M, N lần lượt là giao điểm của KO với AB,CD. 
Áp dụng định lý talet ta có: 
AM/DN=MB/NC(=KM/KN) 
=(AM+MB)/(CN+ND) (t/c dãy tỉ số bằng nhau) =AB/DC. 
=AO/OC=AM/NC. 
Vậy AM/DN=AM/NC hay DN=NC. 
tương tự MB=MA. 
hay ta có OK đi qua trung điểm của AB và CD.

Xin lỗi mình chưa hôc tới định lý talet

ta có ; góc DAB = góc CBA < ABCD là hình thang cân> 

=> 180 độ - góc DAB = 180 độ - góc CBA

=> góc SAB = góc SBA

=> tam giác SAB là tam giác cân tại s 

ta có góc D bằng góc C < ABCD là hình thang >

=> tam giác SCD là tam giác cân tại s

Có thể cách của mk chưa hay lắm! Mà bạn cứ tham khảo nếu thích nha!

Kẻ \(DH,NK\perp AB\)Ta cm được HKND là hình chữ nhật suy ra \(DN=HK=\frac{a}{2}\)

Và \(DH=NK=a\)

Xét \(\Delta ADH\)vuông tại H có \(\widehat{A}=60^o\Rightarrow\widehat{ADH}=30^o\)

suy ra \(AH=\frac{AD}{2}=\frac{a}{2}\)

\(\Rightarrow KM=AM-AH-HK=\frac{AB}{2}-AH-HK\)

\(\Rightarrow KM=\frac{3}{2}a-\frac{a}{2}-\frac{a}{2}=\frac{a}{2}\)

Từ những điều đã chứng minh bạn sẽ cm được \(\Delta ADH=\Delta MNK\left(g.c.g\right)\)

suy ra AD=MN suy ra AMND là hình thang cân

Câu b nè bạn tự vẽ hình nha!

Dễ dàng cm được EI=IC

(có 2 cách 1 là dùng định lí Ta-lét 2 là cm 2 tam giác EIM và CIN bằng nhau theo TH g.c.g)

Ta có AMND là htg cân nên AD=MN=a

suy ra \(IN=\frac{MN}{2}=\frac{a}{2}=NC\)

suy ra tam giác NIC cân tại N có góc N bằng 60 độ suy ra tam giác NIC đều

suy ra IN=IC

Mà IN=IM

và IC=IE suy ra IN=IM=IC=IE

suy ra EMCN là HCN

suy ra EC=MN

mà MN=AD suy ra EC=AD

Mặt khác EC//AD ( do \(\widehat{D}+\widehat{ECD}=120^o+60^o=180^o\)hai góc tcp bù nhau)

nên AECD là hình bình hành suy ra EC=AE suy ra AE=EC=CD=DA

suy ra AECD là hình thoi.

(các số góc dễ tính nên bạn tự tính nha)

c, Ta có AE=AD=a (cm câu b)

EM=IM=\(\frac{a}{2}\)

suy ra \(\frac{EM}{EC}=\frac{\frac{a}{2}}{a}=\frac{a}{2a}=\frac{1}{2}\left(1\right)\)

Và \(\frac{EC}{EB}=\frac{EC}{AB-AE}=\frac{a}{3a-a}=\frac{1}{2}\left(2\right)\)

Từ 1 và 2 suy ra \(\frac{EM}{EC}=\frac{EC}{EB}\)

cm được \(\Delta EMC\)đồng dạng với \(\Delta ECB\)

suy ra \(\widehat{ECB}=\widehat{EMC}=90^o\)

suy ra tam giác ECB vuông tại C

Mấy câu này mk làm qua loa có j ko hiểu thì nhắn tin hỏi mk nha!