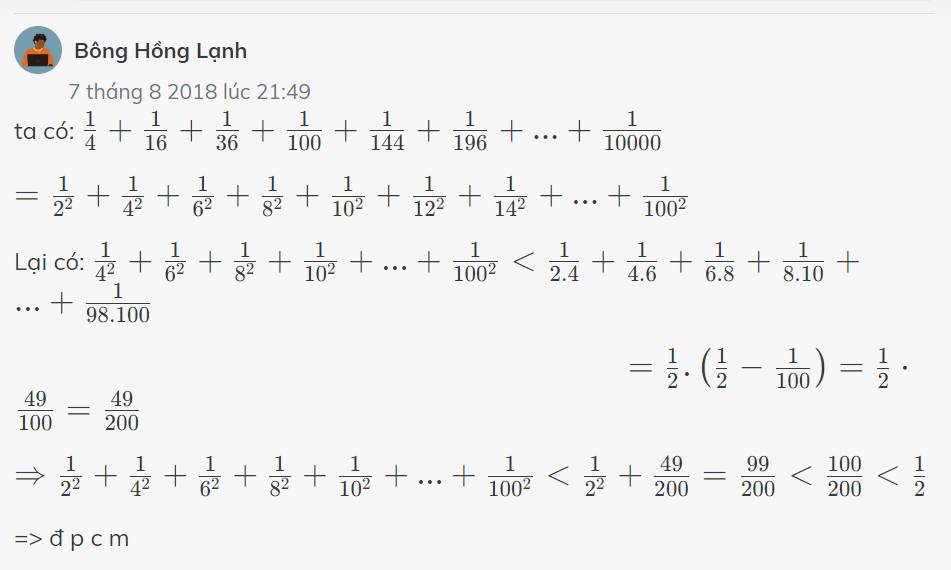dpcm là gì vậy các bồ

dpcm là điều phải chứng minh nha

Ta có :     \(\frac{1}{4}=\frac{1}{2}-\frac{1}{4}\)

                 \(\frac{1}{16}< \frac{1}{4}-\frac{4}{8}\)

                \(\frac{1}{36}< \frac{1}{8}-\frac{1}{12}\)

                \(\frac{1}{64}< \frac{1}{12}-\frac{1}{16}\)

                 \(\frac{1}{100}< \frac{1}{16}-\frac{1}{20}\)

                   \(\frac{1}{144}< \frac{1}{20}-\frac{1}{24}\)

                 \(\frac{1}{196}< \frac{1}{24}-\frac{1}{28}\)

\(\Rightarrow A< \frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+...+\frac{1}{24}-\frac{1}{28}\)

             \(=\frac{1}{2}-\frac{1}{28}< \frac{1}{2}\)

Vậy A<1/12

hình như phân số cuối  phải là 1/324

nếu là 1/324 thì tớ giải nè:

A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324

= 1/4.(1+1/2^2+1/3^2+1/4^2+1/5^2+1/6^2+1/7^2+1/8^2+1/9^2)                                                    <1/4.(1+1/1.2+1/2.3+1/3.4+1/4.5+1/5.6+1/6.7+1/7.8+1/8.9)

= 1/4.(1+1-1/9)

= 1/4.17/9 = 17/36<18/36 = 1/2

=> A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324<1/2

CHO ĐÚNG NHA!!!!!!!!!!!!!!!!

cho dung na

nha bai tren sai day yhemh moi dung ne

A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324

= 1/4.(1+1/2^2+1/3^2+1/4^2+1/5^2+1/6^2+1/7^2+1/8^2+1/9^2) <1/4.(1+1/1.2+1/2.3+1/3.4+1/4.5+1/5.6+1/6.7+1/7.8+1/8.9)

= 1/4.(1+1-1/9)

= 1/4.17/9 = 17/36<18/36 = 1/2

=> A = 1/4+1/16+1/36+1/64+1/100+1/144+1/196+1/256+1/324<1/2

khó hiểu lên thông cảm 

 P = 1/4 + 1/16 + 1/36 + .. + 1/196 = 1/2² + 1/4² + 1/6² +...+ 1/12² + 1/14² 

xét tổng quát với số nguyên dương k ta có: 
(2k-1)(2k+1) = 4k² - 1 < 4k² = (2k)² => 1/(2k)² < 1/(2k-1)(2k+1) 
=> 2/(2k)² < 2 /(2k-1)(2k+1) = 1/(2k-1) - 1/(2k+1) (*) 

ad (*) cho k từ 1 đến 7 
2/2² < 1/1 - 1/3 
2/4² < 1/3 - 1/5 
... 
2/12² < 1/11 - 1/13 
2/14² < 1/13 - 1/15 
+ + cộng lại + + 
2/2² + 2/4² +...+ 2/14² < 1/1 - 1/15 < 1 
=> 2(1/2² + 1/4² +..+ 1/14²) < 1 => P < 1/2 (đpcm)

ta có: \(\frac{1}{4}+\frac{1}{16}+\frac{1}{36}+\frac{1}{100}+\frac{1}{144}+\frac{1}{196}+...+\frac{1}{10000}\)

\(=\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+\frac{1}{12^2}+\frac{1}{14^2}+...+\frac{1}{100^2}\)

Lại có: \(\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+...+\frac{1}{100^2}< \frac{1}{2.4}+\frac{1}{4.6}+\frac{1}{6.8}+\frac{1}{8.10}+...+\frac{1}{98.100}\)

                                                                                                  \(=\frac{1}{2}.\left(\frac{1}{2}-\frac{1}{100}\right)=\frac{1}{2}\cdot\frac{49}{100}=\frac{49}{200}\)

\(\Rightarrow\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\frac{1}{10^2}+...+\frac{1}{100^2}< \frac{1}{2^2}+\frac{49}{200}=\frac{99}{200}< \frac{100}{200}< \frac{1}{2}\)

=> đ p c m

bạn giải dùm mình bài này nhé Tìm x biết: 2+2+2² +2³+2⁴+...+2²⁰¹⁴=2^x.  Ai giúp mình giải bài này với