Sau khi bớt cùng một số k ở cả hai số thì hiệu hai số không đổi. 

Hiệu hai số là: 

\(99-67=32\)

Nếu hai số mới có số thứ nhất là \(3\)phần thì số thứ hai là \(5\)phần.

Hiệu số phần bằng nhau là: 

\(5-3=2\)(phần) 

Số thứ nhất mới là: 

\(32\div2\times3=48\)

Số k là: 

\(67-48=19\)

Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.

Điều kiện x ∈N* và x ≤ 9; y ∈N* và y  ≤  9.

Số có hai chữ số 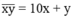 và số đổi chỗ: 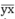= 10y + x

Đổi chỗ hai chữ số thì được một số lớn hơn số đã cho là 63, ta có:

(10y + x) – (10x + y) = 63

Tổng của số đã cho và số mới tạo thành bằng 99, ta có:

(10x + y) + (10y + x) = 99

Ta có hệ phương trình:

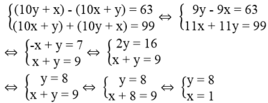
Ta thấy x = 1, y = 8 thỏa điều kiện bài toán.

Vậy số cần tìm là 18.

Ttp

Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.
Điều kiện: x ∈ N* và x ≤ 9; y ∈ N* và y ≤ 9
Số đã cho xy=10x+y; số đổi chỗ yx=10y+x
Đổi chỗ hai chữ số ta được số mới lớn hơn số đã cho 63.
Ta có phương trình: (10y+x)–(10x+y)=63
Tổng của số mới và số đã cho bằng 99, ta có phương trình:
(10x+y)+(10y+x)=99
Ta có hệ phương trình:
(10y+x)–(10x+y)=63
(10x+y)+(10y+x)=99
⇔9y–9x=63
11x+11y=99
⇔–x+y=7
x+y=9
⇔2y=16
x+y=9
⇔y=8
x+8=9
⇔y=8
x=1
Với x =1; y = 8 thỏa mãn điều kiện bài toán
Vậy số đã cho là 18.

bằng 18

Gọi chữ số hàng chục là x, chữ số hàng đơn vị là y.
Điều kiện: x ∈ N* và x ≤ 9; y ∈ N* và y ≤ 9
Số đã cho xy=10x+y; số đổi chỗ yx=10y+x
Đổi chỗ hai chữ số ta được số mới lớn hơn số đã cho 63.
Ta có phương trình: (10y+x)–(10x+y)=63
Tổng của số mới và số đã cho bằng 99, ta có phương trình:
(10x+y)+(10y+x)=99
Ta có hệ phương trình:
(10y+x)–(10x+y)=63
(10x+y)+(10y+x)=99
⇔9y–9x=63
11x+11y=99
⇔–x+y=7
x+y=9
⇔2y=16
x+y=9
⇔y=8
x+8=9
⇔y=8
x=1
Với x =1; y = 8 thỏa mãn điều kiện bài toán
Vậy số đã cho là 18.