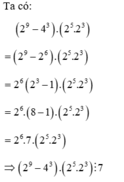Chứng minh rằng: (7206 - 7205+7204) chia hết cho 43

Những câu hỏi liên quan
Chứng minh rằng 2139+3921 chia hết cho 45
Chứng minh rằng 4343-1717 chia hết cho 5
Chứng minh rằng : \(43^{43}-17^{17}\)chia hết cho 5
Ta có:
⇒4343=4320.2+3=4340.433=....1 . ...7 = ...7
⇒1717 = 174.4+1=1716.17=...1 . 17= ....7
⇒4343-1717=...7-...7=....0
⇒\(43^{43}-17^{17}\)⋮5(đpcm)
Đúng 1
Bình luận (0)
Chứng minh rằng:
43^43-37^17 chia hết cho 10
4343-3717=4340.433-3716.37
=(434)10...7-(374)4.37
=.....110...7-....14.37
=.........1...7-.......1.37
=..............7-..........7
=..........0 chia hết cho 10
Vậy 4343-3717 chia hết cho 10
Đúng 0
Bình luận (0)
Chứng minh rằng 43 mũ 43 - 17 mũ 17 chia hết cho 10.
Số có tận cùng là 3 khi nâng lên lũy thừa mũ 4n có tận cùng là 1
Do đó 4343 = 434.10+3=434.10.433= ( .....1 ) . ( ......7 ) = .....7
số có tận cùng là 7 khi nâng lên lúy thùa mũ 4n có tận cũng là 1
Do đó 1717=174.4+1 = 174.4.17= ( ....... 1 ) . ( ........7 ) = .......7
4343-1717 = ......7 - .......7 = ........0
Số có tận cùng là 0 chia hết cho 10
Vậy 4343-1717 chia hết cho 10 ( dpcm )
Đúng 0
Bình luận (0)
Gõ link này là có: http://olm.vn/hoi-dap/question/1081594.html
Đúng 0
Bình luận (0)
Chứng minh rằng:
7) ( 43^43- 17^17) chia hết cho 10
8) ( 7^ 1000- 3^1000) chia hết cho 10
Bài 7 :43^1 =43. tận cùng là số 3
43^2= 1849 tận cùng là số 9
43^3 =79507 tận cùng là số 7
43^4 =3418801 tận cùng là số 1
43^5 = 147008443 tiếp tục tận cùng là số 3
vậy quy luật của nó cứ lặp đi lặp lại theo dãy 4 số 3 - 9 - 7 - 1
ta có 43 chia 4 dư 3. vậy tận cùng của số 43^43 là 7
tương tự ta có số tận cùng của 17^17 là 7.
vậy thì 43^43 - 17^17 ra số có tận cùng là 0. mà số có tận cùng là 0 thì luôn chia hết cho 10 (điều phải chứng minh)
Bài 8 : \(7^{1000}=\left(7^2\right)^{500}=49^{500}\)
\(3^{1000}=\left(3^2\right)^{500}=9^{500}\)
Ta có : lũy thừa tận cùng là 9 khi nâng bậc lũy thừa chẵn nên tận cùng là 1.
=> \(49^{500}\) tận cùng là 1
=> \(9^{500}\) tận cùng là 1
=> (...1) - (....1) = (....0)
Vì tận cùng là 0 nên chia hết cho 10
Vậy 71000 - 31000 chia hết cho 10 (đpcm)
Đúng 0
Bình luận (0)
Bài 7 :43^1 =43. tận cùng là số 3
43^2= 1849 tận cùng là số 9
43^3 =79507 tận cùng là số 7
43^4 =3418801 tận cùng là số 1
43^5 = 147008443 tiếp tục tận cùng là số 3
vậy quy luật của nó cứ lặp đi lặp lại theo dãy 4 số 3 - 9 - 7 - 1
ta có 43 chia 4 dư 3. vậy tận cùng của số 43^43 là 7
tương tự ta có số tận cùng của 17^17 là 7.
vậy thì 43^43 - 17^17 ra số có tận cùng là 0. mà số có tận cùng là 0 thì luôn chia hết cho 10 (điều phải chứng minh)
Bài 8 : 71000=(72)500=4950071000=(72)500=49500
31000=(32)500=950031000=(32)500=9500
Ta có : lũy thừa tận cùng là 9 khi nâng bậc lũy thừa chẵn nên tận cùng là 1.
=> 4950049500 tận cùng là 1
=> 95009500 tận cùng là 1
=> (...1) - (....1) = (....0)
Vì tận cùng là 0 nên chia hết cho 10
Vậy 71000 - 31000 chia hết cho 10 (đpcm)
Đúng 0
Bình luận (0)
chứng minh rằng :
4343-1717 chia hết cho 10
ab+ba chia hết cho 11
CM:\(\overline{ab}+\overline{ba}⋮11\)
Ta có :\(\overline{ab}=10a+b\)
\(\overline{ba}=10b+a\)
\(\Rightarrow\overline{ab}+\overline{ba}=10a+b+10b+a=11a+11b\)
Mà 11b\(⋮\) 11 kí hiệu là 1
11a \(⋮\) 11 kí hiệu là 2
Từ 1 và 2 \(\Rightarrow\) 10a+b+10b+a chia hết cho 11 (t/chất chia hết của 1 tổng)
\(\Rightarrow\overline{ab}+\overline{ba}⋮11\)
Đúng 0
Bình luận (0)
Chứng minh rằng ( 2 9 + 4 3 ) . ( 2 5 .2 3 ) chia hết cho 7.
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: 2 9 + 4 2 . 2 5 .2 3 = 2 9 + 2 4 . 2 5 .2 3 = 2 4 2 5 + 1 . 2 5 .2 3 = 2 4 .33. 2 5 .2 3 ⇒ 2 9 + 4 3 . 2 5 .2 3 ⋮ 11 |
Đúng 0
Bình luận (0)
Chứng minh rằng ( 2 9 + 4 3 ) ( 2 5 . 2 3 ) chia hết cho 7
Chứng minh rằng ( 2 9 − 4 3 ) . ( 2 5 .2 3 ) chia hết cho 7.
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: 2 9 − 4 3 . 2 5 .2 3 = 2 9 − 2 6 . 2 5 .2 3 = 2 6 2 3 − 1 . 2 5 .2 3 = 2 6 . 8 − 1 . 2 5 .2 3 = 2 6 .7. 2 5 .2 3 ⇒ 2 9 − 4 3 . 2 5 .2 3 ⋮ 7 |
Đúng 0
Bình luận (0)
Chứng minh rằng ( 2 9 - 4 3 ) ( 2 5 . 2 3 ) chia hết cho 7