Cho AB là đường kính của đường tròn (O), bán kính OC vuông góc với AB. Gọi D là điểm trên nửa đường tròn (O) không chứa C sao cho BD = OB. Số đo của cung CAD là

Những câu hỏi liên quan
Cho AB là đường kính của đường tròn (O), bán kính OC vuông góc với AB. Gọi D là điểm trên nửa đường tròn (O) không chứa C sao cho BD = OB. Số đo của cung CAD là ......
Chỉ cần viết đáp án là được. help me
cho nửa đưởng tròn tâm o đường kính ab. lấy điểm d trên bán kính ob (khác O,B). gọi h là trung điểm của ad.đường vuông góc tại h với ab cắt nửa đường tròn tại c. đường tròn tâm i đường kính bd cắt tiếp bc tại e a) tứ giác acde là hình gì ? b)c/m tam giác ceh cân tại h và he là tiếp tuyến của (I)
Cho nửa đường tròn tâm (o), đường kính AB=6. Trên đoạn OB lấy điểm H sao cho HB=2HO. Qua H kẻ đường thẳng vuông góc với AB cắt nửa đường tròn tại điểm C. Vẽ đường tâm (I) đường kính OA cắt AC tại D. Gọi E là giao điểm của OC và BD.
a) CM: AD=CD
b) CM: 4 điểm O,D,C,H cùng nằm trên 1 đường tròn
c) CM: BD là tiếp tuyến của đường tròn (I)
GIÚP MÌNH VS
Vì \(\Delta ADC\)nội tiếp đường tròn đường kính AO \(\Rightarrow\widehat{ADO}=90^O\Rightarrow OD⊥AC\left(1\right)\)mà \(\Delta ABC\)nội tiếp đường tròn (O) \(\Rightarrow\widehat{ACB}=90^O\Rightarrow BC⊥AC\left(2\right)\)từ 1 và 2 có \(OD\downarrow\uparrow BC\)Mà O là trung điểm BC thì D sẽ phải là trung điểm AC => AD = DCdo \(OH⊥BC\Rightarrow\widehat{CHO}=90^0\left(3\right)\)Mà \(\widehat{ODC}=90^0\left(4\right)\)TỪ 3 và 4 có D và H nhìn OC dưới cùng một góc vuông nên DOHC nội tiếp đường tròn đường kính OCVì \(OA=OB=OC=\frac{AB}{2}=3,HB=2OH\Rightarrow HB=\frac{2}{3}OB=\frac{2.3}{3}=2\).Theo hệ thức lượng trong tam giác vuông \(\Delta BCA\)có \(BC=\sqrt{HB.AB}=\sqrt{2.6}=\sqrt{12}\)Và HA=AB-HB=6-2=4 => \(AC=\sqrt{AH.AB}=\sqrt{4.6}=2\sqrt{6}\Rightarrow DC=\frac{AC}{2}=\frac{2\sqrt{6}}{2}=\sqrt{6}\)Xét Vuông \(\Delta DCB\)có:\(BD^2=DC^2+BC^2=6+12=18\),\(ID=IO=\frac{OA}{2}=\frac{3}{2}\),\(IB=IO+OB=\frac{3}{2}+3=\frac{9}{4}\)ta có :\(ID^2+BD^2=\frac{9}{4}+18=\frac{81}{4}=IB^2\)Vậy theo hệ thức lượng trong tam giác vuông có \(\Delta IDB\)Vuông tại D \(\Rightarrow ID⊥BD\)Mà ID là bán kính của (I) => BD là tiếp tuyến của (I)
Đúng 0
Bình luận (0)
Cho đường tròn (O), các bán kính OA, OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM = BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng: OC vuông góc với AB
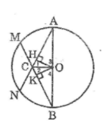
Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao (tính chất tam giác cân)
Suy ra: OC ⊥ AB
Đúng 2
Bình luận (0)
cho đường tròn (O) tâm O, đường kính AB. lấy M là trung điểm của OB, vẽ đường (M) tâm M bán kính MB. gọi d là đường thẳng đi qua M và vuông góc với AB. trên (O) lấy điểm D sao cho dây BD cắt d tại N (D không trùng với A và N ). đường thẳng AN cắt (O) tại điểm thứ hai là C, đường thẳng OC cắt (M) tại điểm thứ hai là P a chứng minh tứ giác ADNM là tứ giác nội tiếp b chứng minh cung BC của (O) và cung BP của (M) có độ dài bằng nhau c chứng minh góc MCD góc AOD
Đọc tiếp
cho đường tròn (O) tâm O, đường kính AB. lấy M là trung điểm của OB, vẽ đường (M) tâm M bán kính MB. gọi d là đường thẳng đi qua M và vuông góc với AB. trên (O) lấy điểm D sao cho dây BD cắt d tại N (D không trùng với A và N ). đường thẳng AN cắt (O) tại điểm thứ hai là C, đường thẳng OC cắt (M) tại điểm thứ hai là P a chứng minh tứ giác ADNM là tứ giác nội tiếp b chứng minh cung BC của (O) và cung BP của (M) có độ dài bằng nhau c chứng minh góc MCD = góc AOD
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm D trên bán kính OB. Gọi H là trung điểm của AD, đường vuông góc với AB tại H cắt nửa đường tròn tại C, vẽ đường tròn tâm I đường kính BD cắt CB tại E.
a, Tứ giác ACED là hình gì?
b, C/minh: tam giác HCE cân.
c, C/minh: HE là tiếp tuyến của đường tròn tâm I.
xdbscasfv jzdr6535943465gthzgh
Cho nửa đường tròn tâm O đường kính AB C là 1 điểm thuộc nửa đường tròn H là hình chiếu của C trên AB . Qua trung điểm M của CH kẻ đường vuông góc với OC cắt nửa đường tròn tại D và E . CMR AB là tiếp tuyến đường tròn tâm C bán kính CD
Tôi cũng có bài khó giống ý hệt bạn,vậy bạn có hướng làm chưa
Đúng 0
Bình luận (0)
Cho đường tròn (O) và hai bán kính OA và OB vuông góc với nhau. Gọi M và N là hai
điểm trên cung nhỏ AB sao cho AM = BN và C là giao điểm của hai đường thẳng AM và BN.
Chứng minh rằng: AB ⊥ OC.
Cho nửa đường tròn tâm O, đường kính AB. Lấy OA làm đường kính, vẽ nửa đường tròn nằm trên nửa mặt phẳng bờ AB chứa nửa đường tròn tâm O. Trên nửa đường tròn đường kính OA lấy điểm C không trùng với A và O, tia OC cắt nửa đường tròn tâm O tại D. Vẽ DH vuông góc với AB. CHứng minh AHCD là hình thang cân
Cho nửa đường tròn tâm O đường kính AB = 20cm . C là 1 điểm chính giữa của nửa đường tròn. Điểm H thuộc bán kính OA sao cho OH = 6cm. Đường vuông góc với OA tại H cắt nửa đường tròn ở D. Vẽ dây AE // DC. Gọi K là hình chiếu của E trên AB. Tính diện tích tam giác AEK

















