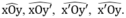1.Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.2. Cho hai đường thẳng xx, yy cắt nhau tại O.a) Chứng minh hai tia phân giác Ot, Ot của một cặp góc kề bù tạo thành một góc vuông.b) Chứng minh rằng: Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot thì M cách đều hai đường thẳng xx và yy.c) Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx, yy thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot.d) Kh...
Đọc tiếp
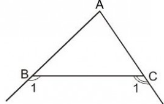
1.Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
2.
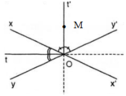
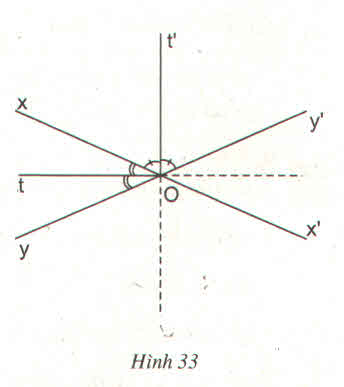
Cho hai đường thẳng xx', yy' cắt nhau tại O.
a) Chứng minh hai tia phân giác Ot, Ot' của một cặp góc kề bù tạo thành một góc vuông.
b) Chứng minh rằng: Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot' thì M cách đều hai đường thẳng xx' và yy'.
c) Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx', yy' thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot'.
d) Khi M ≡ O thì khoảng cách từ M đến xx' và yy' bằng bao nhiêu?
e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau xx', yy'.
~giải_giúp_mk_2_BT_này_vs_C.ơn_mb_nhìu~











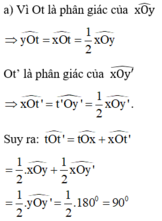






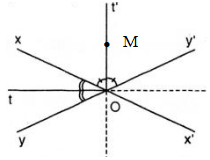








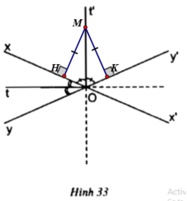
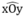 nên M cách đều hai tia Ox và Oy
nên M cách đều hai tia Ox và Oy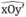 nên M cách đều hai tia Ox, Oy’
nên M cách đều hai tia Ox, Oy’