A, B, C, D là những số có hai chữ số.
A . B = 665.
C . D = 476.
B .C = 595.
Tính A2 + B2 + C2 + D2
Những câu hỏi liên quan
A,B,C,D là những số có hai chữ số
A.B=665
C.D=476
B.C=595
Tính A2+B2+C2+D2
chú ý : A2 là A mũ 2 nha , mấy cái khác cũng vậy
1/A,B,C,D là những số có hai chữ số.
A*B=665
C*D=476
B*C=595
Tính A^2+B^2+C^2+D^2
A, B, C, D là những số có hai chữ số.
A . B = 665.
C . D = 476.
B .C = 595.
Tính A2 + B2 + C2 + D2
1/ A, B, D là những số có 2 chữ số.
A x B= 665
C x D= 476
B x C= 595
Tính: A2 + B2+ C2+ D2
A, B, C, D là những số có hai chữ số.
A. B = 665.
C. D = 476.
Tính A2 + B2 + C2 + D2
Bài 5:
Cho a,b,c,da,b,c,d là các số thực thỏa mãn {a+b+c+d=0a2+b2+c2+d2=2{a+b+c+d=0a2+b2+c2+d2=2
Tìm GTLN của P=abcd.
Bài 6:
Cho a,b,c≥0a,b,c≥0 thỏa mãn a+b+c=1.a+b+c=1. Tìm giá trị lớn nhất của biểu thức:P=abc(a2+b2+c2)
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
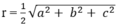
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
Đúng 0
Bình luận (0)
Tìm a,b,c,d thỏa mãn
a2+b2+c2+d2+1=a×(b+c+d+1)
\(a^2+b^2+c^2+d^2+1=a\left(b+c+d+1\right)\)
\(\Leftrightarrow4a^2+4b^2+4c^2+4d^2+4=4ab+4ac+4ad+4a\)
\(\Leftrightarrow a^2-4ab+4b^2+a^2-4ac+4c^2+a^2-4ad+4d^2+a^2-4a+4=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\a=2c\\a=2d\\a=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=c=d=1\end{matrix}\right.\).
Vậy \(\left(a,b,c,d\right)=\left(2,1,1,1\right)\)
Đúng 1
Bình luận (0)
28 tháng 1 2023 lúc 22:21
Cho a, b, c, d, q, p thỏa mãn p2 + q2 - a2 - b2 - c2 - d2 > 0. Chứng minh rằng : ( p2 - a2 - b2 )( q2 - c2 - d2 ) ≤ ( pq- ac - bd )2