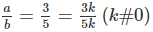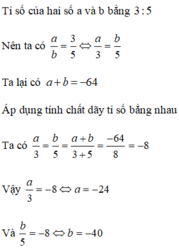Gọi hai số phải tìm là a và b (b ≠ 0)

Ta có: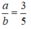 

Đặt a = 3k suy ra b = 5k, do đó:

a2 - b2 = (3k)2 - (5k)2 = 9k2 – 25k2 = -16k2.

Theo đề bài có a2 – b2 = -64, suy ra -16k2 = -64,

suy ra k2 = 4 nên k = 2 hoặc k = -2.

Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10

Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = -10

Vì hiệu bình phương của chúng là -64

nên hiệu cùa chúng là : 8 ( hoặc -8 )

Gọi 2 số đó là a và b

Có:

\(\frac{a}{b}=\frac{3}{5}\) 

\(\Rightarrow a=\frac{3}{5}b\) 

Hiệu hai bình phương của chúng là:

\(a^2-b^2=-64\)

\(\Rightarrow\left(\frac{3}{5}b\right)^2-b^2=-64\)

\(\frac{9}{25}b^2-b^2=-64\)

\(\Rightarrow\frac{-16}{25}b^2=-64\)

\(b^2=100\)

\(\Rightarrow b\in\left\{-10;10\right\}\)

Với b = -10 \(\Rightarrow a=\frac{3}{5}.\left(-10\right)=-6\)

Với b =10 \(\Rightarrow a=\frac{3}{5}.10=6\)

Gọi hai số phải tìm là a và b (b \(\ne\) 0).

Ta có \(\frac{a}{b}=\frac{3}{5}=\frac{3k}{5k}\) ( k \(\ne\) 0).

Vậy a = 3k và b = 5k. 

Mà a² - b² = -64 nên (3k)² - (5k)² = -64

\(\Leftrightarrow\) 9k² - 25k² = 64 \(\Leftrightarrow\) (9 - 25).k² = -64 \(\Leftrightarrow\) -16k² = -64

\(\Rightarrow\) k² = -64 : 16 \(\Leftrightarrow\) k² = 4 

\(\Leftrightarrow\) k = + 2.

Với k = 2 thì a = 3 . 2 = 6 và b = 5 . 2 = 10

Với k = -2 thì a = 3 . (-2) = -6 và b = 5 . (-2) = -10

                   Vậy a = 6 và b = 10 hoặc a = -6 và b = -10

Hiệu số phần bằng nhau là :

5 - 3 = 2 ( phần )

Số thứ nhất là :

( - 64 ) : 2 x 3 = - 96

Số thứ hai là :

( - 96 ) + ( - 64 ) = - 160

Đáp số : Số thứ nhất : - 96

             Số thứ hai : - 160

Gọi 2 số đó là a và b.

Ta có:

\(\frac{a}{b}=\frac{3}{5}=\frac{3k}{5k}\)=> a = 3k

                         => b = 5k (k thuộc Z, k khác 0)

Vì hiệu bình phương của chúng là -64.

=> a² - b² = -64

=> (3k)² - (5k)² = -64

=> 9k² - 25k² = -64

=> -16k² = -64

=> k² = (-64) : (-16)

=> k² = 4

=> k = 2 hoặc -2 

=> \(\frac{a}{b}=\frac{3.2}{5.2}=\frac{6}{10}\)

hoặc \(\frac{a}{b}=\frac{3.\left(-2\right)}{5.\left(-2\right)}=\frac{-6}{-10}\)

Vậy 2 số đó là 6 và 10 hoặc -6 và -10

Gọi hai số cần tìm là a và b \(\left(a\ne0\right)\)

Ta có : \(\dfrac{a}{b}=\dfrac{3}{5}=\dfrac{3k}{5k}\left(k\ne0\right)\)

Vậy \(a=3k , b=5k\) ,do đó :

\(a^2-b^2=\left(3k\right)^2-\left(5k\right)^2=-64\)

\(9k^2-25k^2=-64\)

\(-16k^2=-64\)

\(k^2=4\)

\(k=\pm2.\)

Với \(k=2\) thì \(a=3.1=6,b=5.2=10\)

Với \(k=-2\) thì \(a=3.\left(-2\right)=-6,b=5.\left(-2\right)=-10\)

Gọi hai số phải tìm là a và b (b ≠ 0)

Ta có

Vậy a = 35; b = 5k, do đó:

a² - b² = (3k)² - (5k)² = -64

⇔9k² - 25k² = -64

⇔-16k² = -64

⇔k² = 4

⇔k = -2 hoặc k = 2

Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10

Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = 10

Gọi hai số phải tìm là a và b (b ≠ 0)

Ta có

Vậy a = 35; b = 5k, do đó:

a² - b² = (3k)² - (5k)² = -64

⇔9k² - 25k² = -64

⇔-16k² = -64

⇔k² = 4

⇔k = -2 hoặc k = 2

Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10

Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = 10

Số bé trừ lớn là -64 --> Giả sử a-b=-64 --> b-a=64 Có a:b=3:5. Tính a,b khi biết hiệu và tích được a=96, b=160.  

Gọi 2 số cần tìm là a và b 

theo đề bài ta có :

a/b = 3/5 => a = 3k;b = 5k

a^2-b^2 = -64 => (3k)^2 - (5k)^2 = -64

=> 9k^2 - 25k^2 = -64

=> -16k^2 = -64 

=> k^2 = 4 => k = +2;-2

*, k = 2 => a = 6 ; b = 10

*, k = -2 => a = -6 ; b = -10  

ghi loi giai giup to voi