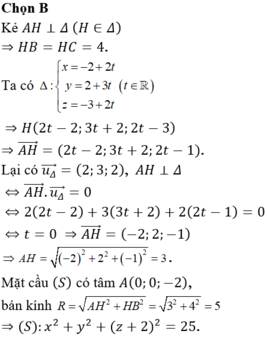cho đường thẳng Δ : x + y - 2 = 0 và điểm A( 2; 2). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho khoảng cách từ A đến M nhỏ nhất.
Những câu hỏi liên quan
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
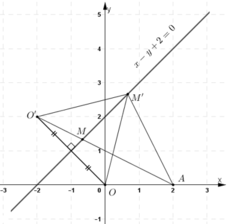
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận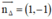 
là một vtpt ⇒ (Δ) nhận 
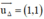là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận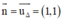 
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
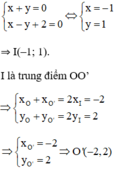
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là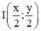 
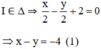
+ (Δ) nhận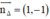 
là một vtpt ⇒ (Δ) nhận 
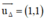là một vtcp.
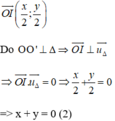
Từ (1) và (2) ta có hệ phương trình
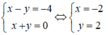
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
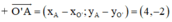
⇒ O’A nhận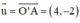 
là một vtcp
⇒ O’A nhận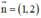 
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
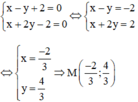
Vậy điểm M cần tìm là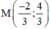 
Đúng 0
Bình luận (0)
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0). Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
Trước hết ta thấy O, A nằm trên cùng một mặt phẳng bờ \(\Delta\).
Qua A kẻ đường thẳng d vuông góc với \(\Delta\) tại H.
Đường thẳng d có phương trình: \(x+y-2=0\)
\(\Rightarrow H\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow H=\left(0;2\right)\)
Gọi A' là điểm đối xứng với A qua d
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=-2\\y_{A'}=2y_H-y_A=4\end{matrix}\right.\Rightarrow A'=\left(-2;4\right)\)
\(\Rightarrow OA'=2\sqrt{5}\)
Phương trình đường thẳng OA': \(2x+y=0\)
Khi đó: \(OM+MA=OM+MA'\ge OA'=2\sqrt{5}\)
\(min=2\sqrt{5}\Leftrightarrow M\) là giao điểm của \(\Delta\) và OA'
\(\Leftrightarrow M\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\2x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{2}{3};\dfrac{4}{3}\right)\)
Đúng 1
Bình luận (0)
Lời giải:
Vì $M$ thuộc $\Delta$ nên $M$ có tọa độ $(a-2,a)$
Độ dài đường gấp khúc $OMA$ là:
$OM+MA=\sqrt{a^2+(a-2)^2}+\sqrt{(a-4)^2+a^2}$
$=\sqrt{2}.(\sqrt{(a-1)^2+1}+\sqrt{(2-a)^2+2^2})$
$\geq \sqrt{2}.\sqrt{(a-1+2-a)^2+(1+2)^2}$ (theo BĐT Mincopxky)
$=2\sqrt{5}$
Vậy $OMA$ min bằng $2\sqrt{5}$. Giá trị này đạt tại $a=\frac{4}{3}$
Vậy $M(\frac{-2}{3},\frac{4}{3})$
Đúng 2
Bình luận (2)
Cho đường tròn (C): (x - 1
)
2
+ (y + 3
)
2
10 và đường thẳng Δ: x + y + 1 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng: A.
19
2
B.
38
C.
19
2
D.
38
2
Đọc tiếp
Cho đường tròn (C): (x - 1 ) 2 + (y + 3 ) 2 = 10 và đường thẳng Δ: x + y + 1 = 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng:
A. 19 2
B. 38
C. 19 2
D. 38 2
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
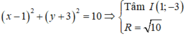
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
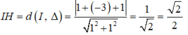
Xét tam giác AIH vuông tại H ta có:
A H 2 + I H 2 = A I 2 ⇒ A H 2 = A I 2 - I H 2
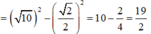
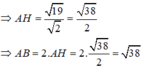
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x -3 + 2t, y 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 0.a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
A nhé
hihhihihiihihihhiihhiihihihih
Cho (C) : x2+y2-2x-2my+m2-24=0 có tâm I và đường thẳng Δ: mx + 4y = 0. Tìm m biết đường thẳng Δ cắt (C) tại 2 điểm phân biệt A,B thoả mãn SIAB = 12.
Đường tròn (C) có tâm I(1; m), bán kính R = 5.
Gọi H là trung điểm của dây cung AB.
Ta có IH là đường cao của tam giác IAB:
Đúng 0
Bình luận (1)
Tìm toạ độ giao điểm của đường tròn (C) :\(x^2+y^2-25=0\) và đường thẳng Δ: x+y-3=0
Giao điểm của \(\left(C\right)\) và \(\left(d\right)\) có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x^2+y^2-25=0\\x+y-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2-2xy-25=0\\x+y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=-8\\x+y=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=\dfrac{3+\sqrt{41}}{2}\\y=\dfrac{3-\sqrt{41}}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}x=\dfrac{3-\sqrt{41}}{2}\\y=\dfrac{3+\sqrt{41}}{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(\dfrac{3+\sqrt{41}}{2};\dfrac{3-\sqrt{41}}{2}\right)\\\left(\dfrac{3-\sqrt{41}}{2};\dfrac{3+\sqrt{41}}{2}\right)\end{matrix}\right.\)
Kết luận: Tọa độ giao điểm: \(\left\{{}\begin{matrix}\left(\dfrac{3+\sqrt{41}}{2};\dfrac{3-\sqrt{41}}{2}\right)\\\left(\dfrac{3-\sqrt{41}}{2};\dfrac{3+\sqrt{41}}{2}\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
1
2
y
1
z
-
2
1
, mặt phẳng (P): x + y - 2z + 5 0 và A (1; -1; 2). Đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vectơ chỉ phương của Δ là:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 1 2 = y 1 = z - 2 1 , mặt phẳng (P): x + y - 2z + 5 = 0 và A (1; -1; 2). Đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vectơ chỉ phương của Δ là:
A . u → = 2 ; 3 ; 2
B . u → = 1 ; - 1 ; 2
C . u → = - 3 ; 5 ; 1
D . u → = 4 ; 5 ; - 13
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng
∆
:
x
-
1
2
y
1
z
-
3
-
1
,
∆
:
x
1
y...
Đọc tiếp
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 .
Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:
Chọn C
Gọi d là đường thẳng cần tìm.
Đường thẳng cần tìm qua A và nhận 
là véc tơ chỉ phương nên có phương trình:
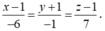
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho điểm A (0; 0; -2) và đường thẳng
∆
:
x
+
2
2
y
-
2
3
z
+
3
2
. Phương trình mặt cầu tâm A, cắt Δ tại hai điểm B và C sao cho BC 8 là:
A
.
...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho điểm A (0; 0; -2) và đường thẳng ∆ : x + 2 2 = y - 2 3 = z + 3 2 . Phương trình mặt cầu tâm A, cắt Δ tại hai điểm B và C sao cho BC = 8 là:
A . S : x 2 + y 2 + z + 2 2 = 16
B . S : x 2 + y 2 + z + 2 2 = 25
C . S : x + 2 2 + y + 3 2 + z + 1 2 = 16
D . S : x + 2 2 + y 2 + z 2 = 25
