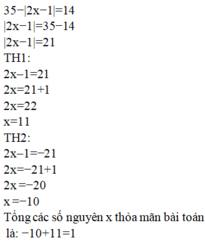số các số nguyên x thỏa mãn 1/3+3/35<x/210<4/7+3/5+1/3 là:

Những câu hỏi liên quan
Tổng các số nguyên x thỏa mãn 35−|2x−1|=14 là:
A. 1
B. 0
C. 15
D. 21
1. Chữ số tận cùng của tích : ( -1).(-2).(-3)...(-2013).(-2014)
2. Số các số nguyên x thỏa mãn 4(x+2) chia hết cho (x+1) là
3. Số các số nguyên x thỏa mãn !-2x+3! = 8 ( !: giá trị tuyệt đối)
Câu hỏi 3:Số nguyên x thỏa mãn x + ( -47) -33 - 35 là Câu hỏi 4:Số nguyên x thỏa mãn x - ( -25 - 17 - x ) 6 + x là Câu hỏi 5:Tập hợp các số nguyên x thỏa mãn |( x - 23)( x + 12)| 0 là (Nhập các phần tử theo thứ tự tăng dần, cách nhau bởi dấu ; )Câu hỏi 9:Với p là số nguyên tố lớn hơn 3 thì số dư của A ( p - 1)( p + 1 ) + 3 khi chia cho 24 là Hãy điền dấu ; ; vào chỗ ... cho thích hợp nhé !Câu hỏi 10:( -17 ) - ( -3) ....... ( -16 ) + 5 - ( -3 )
Đọc tiếp
Câu hỏi 3:
Số nguyên x thỏa mãn x + ( -47) = -33 - 35 là
Câu hỏi 4:
Số nguyên x thỏa mãn x - ( -25 - 17 - x ) = 6 + x là
Câu hỏi 5:
Tập hợp các số nguyên x thỏa mãn |( x - 23)( x + 12)| = 0 là
(Nhập các phần tử theo thứ tự tăng dần, cách nhau bởi dấu ";" )
Câu hỏi 9:
Với p là số nguyên tố lớn hơn 3 thì số dư của A = ( p - 1)( p + 1 ) + 3 khi chia cho 24 là
Hãy điền dấu >; < ; = vào chỗ ... cho thích hợp nhé !
Câu hỏi 10:
( -17 ) - ( -3) ....... ( -16 ) + 5 - ( -3 )
Bài 1: Có tất cả_____cặp số nguyên (x;y) thỏa mãn 2/x/ + 3/y/ = 13.
Bài 2: Số các cặp số nguyên (x;y) thỏa mãn xy + 3x = 7y + 22 là...?
mk cần gấp ạ!
1.
\(2\left|x\right|+3\left|y\right|=13\Rightarrow\left|x\right|=\dfrac{13-3\left|y\right|}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\left|y\right|\le\dfrac{13}{3}\\\left|y\right|\text{ là số lẻ}\end{matrix}\right.\) \(\Rightarrow\left|y\right|=\left\{1;3\right\}\)
- Với \(\left|y\right|=1\Rightarrow\left|x\right|=5\Rightarrow\) có 4 cặp
- Với \(\left|y\right|=3\Rightarrow\left|x\right|=2\) có 4 cặp
Tổng cộng có 8 cặp số nguyên thỏa mãn
2.
\(x\left(y+3\right)=7y+21+1\)
\(\Leftrightarrow x\left(y+3\right)-7\left(y+3\right)=1\)
\(\Leftrightarrow\left(x-7\right)\left(y+3\right)=1\)
\(\Rightarrow\left(x;y\right)=\left(6;-4\right);\left(8;-2\right)\) có 2 cặp
Đúng 3
Bình luận (0)
Tìm các số nguyên \(x,y\) thỏa mãn \(3^x-y^3=1\)
Xét \(x=0\Rightarrow y=0\), \(x=1\Rightarrow y^3=2\), vô lí. \(x=2\Rightarrow y=2\).
Với \(x\ge3\), ta viết lại pt đã cho như sau:
\(y^3=3^x-1\).
Ta thấy \(y\equiv2\left[3\right]\) \(\Rightarrow y=3z-1\left(z\inℕ^∗\right)\)
\(\Rightarrow\left(3z-1\right)^3=3^x-1\)
\(\Leftrightarrow27z^3-27z^2+9z-1=3^x-1\)
\(\Leftrightarrow27z^3-27z^2+9z=3^x\)
\(\Leftrightarrow9z^3-9z^2+z=3^{x-2}\)
\(\Leftrightarrow z\left(9z^2-9z+1\right)=3^{x-2}\)
Do \(9z^2-9z+1⋮̸3\) nên \(\left\{{}\begin{matrix}z=3^{x-2}\\9z^2-9z+1=1\end{matrix}\right.\), vô lí do \(z\inℕ^∗\)
Vậy với \(x\ge3\) thì pt đã cho không có nghiệm nguyên.
Do đó pt đã cho có cặp nghiệm nguyên \(\left(x,y\right)\in\left\{\left(0;0\right);\left(2;2\right)\right\}\)
Đúng 1
Bình luận (0)
- Nếu x < 0 => y không nguyên
- Nếu x = 0 => y = 0
- Nếu x = 1 => y không nguyên
- Nếu x = 2 => y = 2
- Nếu x > 2 pt => 3x = y3 + 1 ( Vì x > 2 => y3 > 9 )
Ta suy ra dư 1
hoặc hoặc ( k là số nguyên dương ) (1)
Mặt khác, ta cũng có
( m nguyên dương ) (2)
Từ (1) và (2) => vô nghiệm ( Vì từ (2) không thỏa (1) )
Vậy phương trình có 2 cặp nghiệm nguyên không âm là ( 0;0 ) và ( 2;2 )
Đúng 0
Bình luận (0)
Tìm các số nguyên x thỏa mãn (x + 3) ⋮ (x + 1)
A. x ∈ {-3; -2; 0; 1}
B. x ∈ {-1; 0; 2; 3}
C. x ∈ {-3; 0; 1; 2}
D. x ∈ {-2; 0; 1; 3}
Đáp án là A
Ta có: x + 3 = (x + 1) + 2
Vì (x + 3) ⋮ (x + 1), (x + 1) ⋮ (x + 1) ⇒ 2 ⋮ (x + 1)
Do đó, x + 1 = ±1 hoặc x + 1 = ±2
Nếu x + 1 = ±1 thì x = 0 hoặc x = -2
Nếu x + 1 = ±2 thì x = 1 hoặc x = -3
Vậy x ∈ {-3; -2; 0; 1}
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn thỏa mãn:2x-3y=1
các bn giúp mình giải 1 số bài tập này nhé :
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho n-2
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho 2n -2
-tìm các số nguyên x thỏa mãn x lớn hơn hoặc bằng -21/7 và x bé hơn hoặc bằng 3
-tìm các số tự nhiên x,y thỏa mãn x-1 chia hết cho y , y-1 chia hết cho x
Số các số nguyên x thỏa mãn 1/3+3/5<x/210<4/7+3/5+1/3