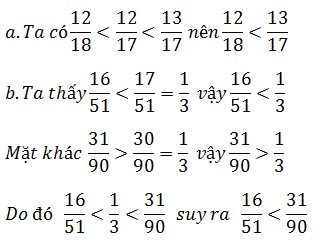qui đồng mẫu các phân số sau: 11/18; -5/9; -7/12

Những câu hỏi liên quan
quy đồng mẫu các phân số sau -7/12 -11/18
MSC: 36
\(-\dfrac{7}{12}=-\dfrac{7\times3}{12\times3}=\dfrac{21}{36}\)
\(-\dfrac{11}{18}=-\dfrac{11\times2}{18\times2}=-\dfrac{22}{36}\)
Đúng 3
Bình luận (1)
MC = BCNN(12,18)=36
-7/12=-7/12×3/3=-21/36
-11/18=-11/18×2/2=-22/36
Đúng 0
Bình luận (0)
Không qui đồng mẫu số,không qui đồng tử số,hãy so sánh các phân số sau
a , 12 18 ; 13 17 b , 16 51 ; 31 90
quy đồng mẫu số các phân số sau 11/18 ; -5/9 ; -7/12
/\_/\
(0-0)
/v > ! |0v3 y0n
\(\dfrac{22}{36};-\dfrac{20}{36};-\dfrac{21}{36}\)
Đúng 3
Bình luận (0)
Qui đồng mẫu thức các phân thức sau (có thể áp dụng qui tắc đổi dấu với các phân thức để tìm mẫu thức chung thuận tiện hơn):
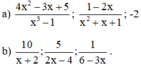
a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:
x3 – 1 = (x – 1)(x2 + x + 1)
x2 + x + 1 = x2 + x + 1
⇒ MTC = (x – 1)(x2 + x + 1) = x3 – 1
+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)
(x3 – 1) : (x3 – 1) = 1
(x3 – 1) :( x2 + x + 1) = x - 1
(x3 – 1) : 1 = x3 – 1
+ Quy đồng :
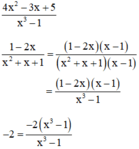
b) Ta có:
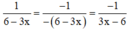
+ Phân tích mẫu thức thành nhân tử để tìm MTC
x + 2 = x + 2
2x – 4 = 2.(x – 2)
3x – 6 = 3.(x – 2)
⇒ MTC = 6.(x + 2)(x – 2)
+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)
6(x + 2)(x – 2) : (x + 2) = 6(x – 2)
6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)
6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)
+ Quy đồng:
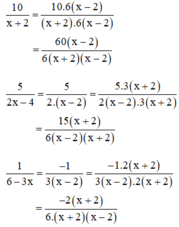
Đúng 0
Bình luận (0)
Qui đồng mẫu số các phân số sau: 36/45;120/45;117/405;632/840;90/135;54/90
So sánh các phân số sau bằng các quy đồng mẫu số hoặc quy đồng tử số:
a)5/8 và 8/9
b)8/12 và 5/9
c)7/12 và 11/18
a) 5/8 < 8/9
b) 8/12 > 5/9
c) 7/12 < 11/18
Đúng 0
Bình luận (0)
Rút gọn rồi qui đồng mẫu các phân số sau:
4.5
+
4.11
8.7
+
4.3
;
−
15.8
+
10.7
5.6
+
20.3
và
2
4
.5...
Đọc tiếp
Rút gọn rồi qui đồng mẫu các phân số sau: 4.5 + 4.11 8.7 + 4.3 ; − 15.8 + 10.7 5.6 + 20.3 và 2 4 .5 2 .7 2 3 .5.7 2 .11
Quy đồng mẫu số các phân số sau ; a) 3 phần 5 và 11 phần 25 ; b) 5 phần 6 và 7 phần 18 ; c) 8 phần 11 và 13 phần 33
Xem chi tiết
So sánh các phân số sau mà không quy đồng tử hoặc mẫu
9/10, 11/14, 3/4, 13/18