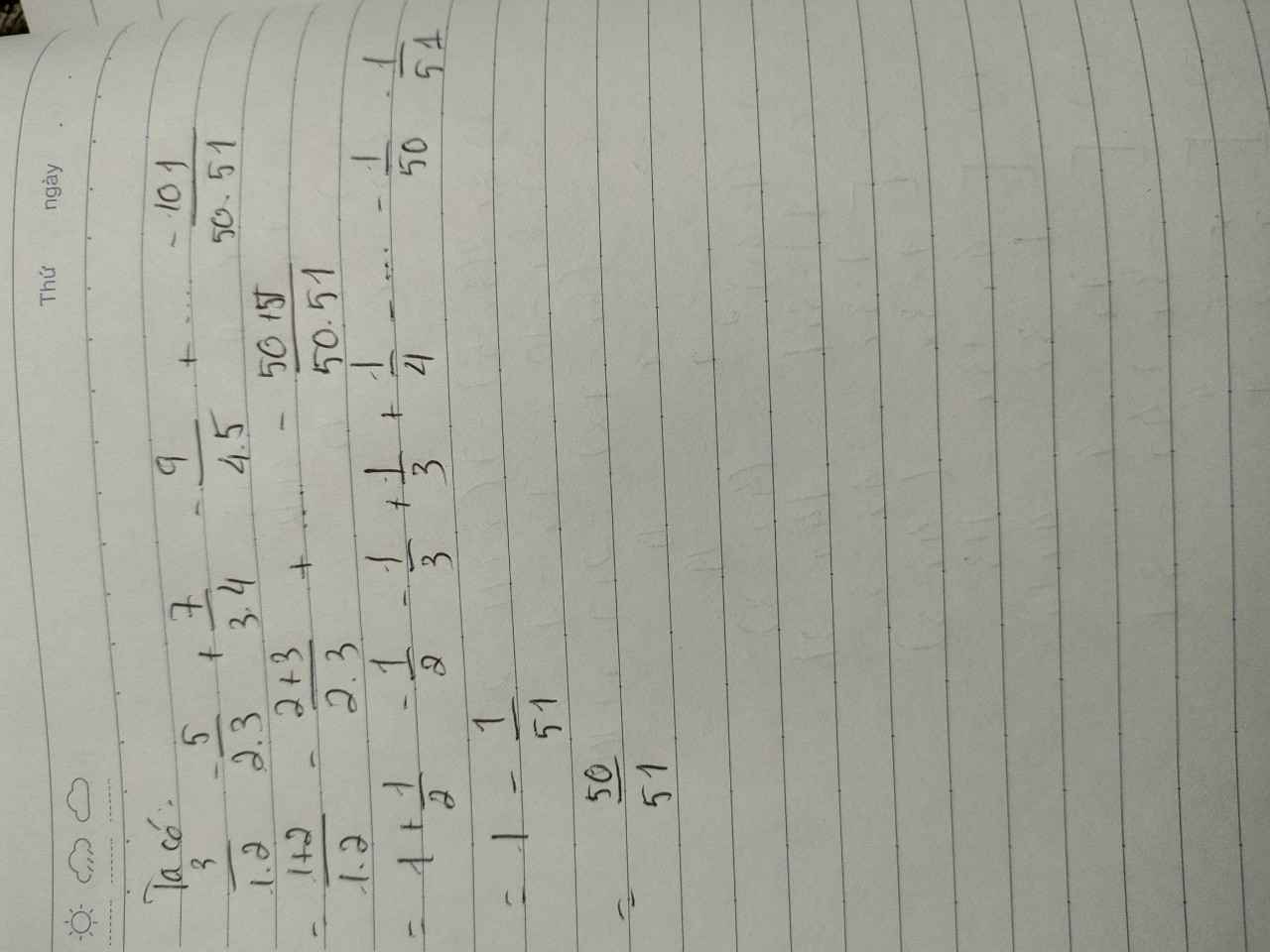tính nhanh:5/1x2 + 5/2x3 + 5/3x4 ...+ 5/98x99 + 5/ 99x100

Những câu hỏi liên quan
\(\dfrac{1}{1x2}\)+ \(\dfrac{1}{2x3}\) + \(\dfrac{1}{3x4}\) +...+ \(\dfrac{1}{98x99}\) + \(\dfrac{1}{99x100}\)
tính nhanh bài này
Đây là dạng tính nhanh tổng các phân số, trong đó mỗi phân số của tổng có tử số bằng hiệu hai thừa số dưới mẫu và mẫu thứ hai của thừa số này là mẫu số thứ nhất của phân số liền kề với nó. Em tách từng phân số thành hiệu hai phân số mà tử số là 1 còn mẫu số là mẫu hai mẫu số của phân số ban đầu. Triệt tiêu các hạng tử giống nhau ta được tổng cần tìm
Dưới đây là cách giải chi tiết em tham khảo nhé em.
A = \(\dfrac{1}{1\times2}\) + \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\)+ .....+ \(\dfrac{1}{99\times100}\)
A = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) +.....+ \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
A = \(\dfrac{1}{1}\) - \(\dfrac{1}{100}\)
A = \(\dfrac{99}{100}\)
Đúng 2
Bình luận (0)
HD: \(\dfrac{1}{nx\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
A= \(1-\dfrac{1}{100}=\dfrac{99}{100}\)
Đúng 2
Bình luận (0)
Tính nhanh :
A = 1/1x2 + 1/2x3 + 1/3x4 + 1/4x5 + ........1/98x99 + 1/99x100 .
ta có :\(\frac{1}{1\cdot2}=\frac{1}{1}-\frac{1}{2}\)
\(\frac{1}{2\cdot3}=\frac{1}{2}-\frac{1}{3}\)
\(\frac{1}{3\cdot4}=\frac{1}{3}-\frac{1}{4}\)
......
\(\frac{1}{99\cdot100}=\frac{1}{99}-\frac{1}{100}\)
=> \(A=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=>A=\frac{1}{1}-\frac{1}{100}=\frac{100}{100}-\frac{1}{100}=\frac{99}{100}\)
Đúng 0
Bình luận (0)
Tính:1/1x2 + 1/2x3 + 1/3x4 + ... + 1/98x99 + 1/99x100
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}\)
\(=\frac{99}{100}\)
Đúng 8
Bình luận (0)
Cho hai số biết rằng bớt số thứ nhất 28 đơn vị thì được số thứ hai va 1/3 số thứ nhất bằng 3/5 số thứ hai.Tìm hai số đó
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
1x2+2x3+3x4+...+98x99+99x100 = ?
Đặt S = 1x2+2x3+3x4+...+98x99+99x100
S x 3 =1x2x3+2x3x3+3x4x3+...+98x99x3+99x100x3
S x 3 =1x2x(3-0)+2x3x(4-1)+3x4x(5-2)+....+98x99x(100-97)+99x100x(101-98)
S x 3 = 1x2x3 + 2x3x4-1x2x3+3x4x5-2x3x4+...+98x99x100-97x98x99+99x100x101-98x99x100
S x 3 = 99x100x101
S x 3 = 999900
S = 333300
Đúng 1
Bình luận (0)
Tính A= 1/1x2+1/2x3+1/3x4+........+1/98x99+1/99x100
Tính:1/(1x2)+1/(2x3)+1/(3x4)+1/(4x5)+...+1/(98x99)+1/(99x100)
\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+....+\frac{1}{99\times100}\)
\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\frac{1}{1}-\frac{1}{100}\)
\(\frac{100-1}{100}\)
\(\frac{99}{100}\)
Đúng 1
Bình luận (0)
\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{99\times100}\)
\(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\frac{1}{1}-\frac{1}{100}\)
\(\frac{100-1}{100}\)
\(\frac{99}{100}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
S= 1x2+2x3+3x4+4x5+...+98x99+99x100
Gọi biểu thức trên là A, ta có :
A = 1x2 + 2x3 + 3x4 + 4x5 + ...+ 99x100
A x 3 = 1x2x3 + 2x3x3 + 3x4x3 + 4x5x3 + ... + 99x100x3
A x 3 = 1x2x3 + 2x3x(4-1) + 3x4x(5-2) + 4x5x(6-3) + ... + 99x100x(101-98)
A x 3 = 1x2x3 + 2x3x4 - 1x2x3 + 3x4x5 - 2x3x4 + 4x5x6 - 3x4x5 + ... + 99x100x101 - 98x99x100.
A x 3 = 99x100x101
A = 99x100x101 : 3
A = 333300
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
TÍNH
A= 9/1x2 + 9/2x3 + 9/3x4 +..........+ 9/98x99 + 9/99x100
\(A=\frac{9}{1.2}+\frac{9}{2.3}+\frac{9}{3.4}+....+\frac{9}{98.99}+\frac{9}{99.100}\)
\(A=9\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{98}-\frac{1}{99}+\frac{1}{99}-\frac{1}{100}\right)\)
\(A=9\left(1-\frac{1}{100}\right)\)
\(A=9\cdot\frac{99}{100}=\frac{891}{100}\)
Đúng 0
Bình luận (0)
\(A=9\left(\frac{1}{1x2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\right)\)
=> \(A=9\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\right)\)
=> \(A=9\left(1-\frac{1}{100}\right)=\frac{9.99}{100}=\frac{891}{100}\)
=> A=8,91
Đúng 0
Bình luận (0)
3/1x2-5/2x3+7/3x4-9/4x5+.......-197/98x99