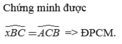Cho tam giác ABC cân tại B. Gọi BE là đường phân giác cùa góc ngoài tại đỉnh B. C/m BE//AC

Những câu hỏi liên quan
Cho tam giác ABC cân tại góc B , Gọi BE là đường phân giác của góc ngoài tại B. C/minh BE//AC
Giải NHANH GỌN LẸ MÌNH C.ƠN TRC
Theo t/chất tam giác cân => góc A= góc C
Vẽ Bx trên tia đối BC có góc xBA là góc ng` tg ABC
=>A+C=xBA
=>Cx2=xBA
Lại có xBE+EBA=xBA
BE là p/giác xBA
->ABE.2=xBA=C.2
=>ABE=C ->SLT
=>BE/AC
Đúng 0
Bình luận (0)
1. Tam giác ABC cân tại A có góc A=100*. Lấy các điểm D và E sao cho trên cạnh BC có BD=BA, CE=CA. Tính góc DAE
2.Cho tam giác ABC cân tại góc B . Gọi BE là đường phân giác của góc ngoài tại B . C/minh BE//AC
Cho tam giác ABC cân tại B.Gọi BE là đường phân giác của góc ngoài tại đỉnh B.CMR:BE//AC
Vì BE là tia pg của góc ngoài tại đỉnh B=>góc ABE= góc EBH=>góc ABE=1/2 góc ABH(1)
Xét góc ngoài ABH của \(\Delta\)ABC tại đỉnh B ta có: góc ABH= góc BAC+ACB
mà \(\Delta\)ABC là tam giác cân tại B=> góc BAC=ACB
=>góc BAC=1/2 góc ABH(2)
Từ (1)và (2)=>góc ABE= góc BAC
Mà 2 góc này ở vị trí so le trong
=>BE//AC
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại B. Gọi BÉ là phân giác của goc ngoài tại đỉnh B
CMR BE//AC
Tam giác ABC cân tại B. Gọi BE là tia phân giác góc ngoài tại B. CMR BE song song với AC
Ta thấy vì BE là tia phân giác ngoài đỉnh B nên góc ABE=gEBH=>gABE=1/2gABH(1)
Xét góc ngoài ABH của tgABC lên đỉnh B ta lại có gABH=gBAC+ACB
Mà theo đề bài tg ABC cân tại B nên BAC=ACB
=>gBAC=1/2gABH(2)
Từ (1) và (2)=>gABE=gBAC
Mà 2 góc này có vị trí so le trong
Nên=> BE//AC
đpcm.
Gọi \(\widehat{DBA}\) là góc ngoài của của \(\Delta BAC\) tại điểm B
Ta có: \(\widehat{DBA}=\widehat{BAC}+\widehat{BCA}\) ( Tính chất góc ngoài của tam giác)
Vì BE là tia phân giác của \(\widehat{DBA}\) nên:
\(\widehat{EBA}=\frac{\widehat{DBA}}{2}=\frac{\widehat{BAC}+\widehat{BCA}}{2}\)
Mà : \(\widehat{BAC}=\widehat{BCA}\) (vì \(\Delta BAC\)cân tại B ) \(\left(1\right)\)
\(\Rightarrow\widehat{EBA}=\frac{2\cdot\widehat{BAC}}{2}=\widehat{BAC}\) \(\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\widehat{BAC}=\widehat{EBA}\)
Mà 2 góc BAC và EBA là 2 góc so le trong
Do đó: \(BE//AC\)
Cho tam giác ABC cân tại B, gọi BE là đường phân giác của góc ngoài tại B.
CMR : BE song song AC
Ta có: B1 + B2 + B3 = 180' (giả thiết)
Mà B2 = B1 => B3 + 2B2 = 180'(1)
Tam giác ABC có: A + B3 + C = 180'
Mà A = C => B3 + 2C = 180'(2)
Từ (1) và (2) => 2B2 = 2C
=> B2 = C => BE song song AC (vì có một cặp góc ở vị trí so le trong bằng nhau)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, AB=15cm,BC=10cm, đường phân giác của góc B cắt ac tại D
a/ tính AD, DC
b/ Đường vuông góc với BD tại B cắt đường Thẳng AC kéo dài tại E. Chứng minh BE là đường Phân giác ngoài tại đỉnh B của tam giác ACB và ính EC, EA,BD
Cho tam giác ABC cân tại B. Gọi Bx là tia phân giác của góc ngoài tại đỉnh B. Chứng minh Bx //AC.
vì tam giác ABC cân tại C(gt)
suy ra: góc A= góc C
góc ZBC là góc ngoài của tam giác ABC
suy ra:góc zBC= gócA + gócC
Mà góc zBC = góc B1 + góc B2
suy ra: gócA+ gócC= gócB1+ góc B2
suy ra: gócB2= gócC
do đó Bx//AC( vì có 2 góc đồng vị bằng nhau )

Đúng 0
Bình luận (0)
1.Cho tam giác ABC có góc A bằng 120 độ, đường phân giác AD. Đường phân giác ngoài tại đỉnh C cắt đường thẳng AB tại K. E là giao điểm của DK và AC. Tính góc BED?
2.Cho tam giác ABC có góc A bằng 120 độ, các đường phân giác AD, BE, CF.
a.Chứng minh DE là phân giác ngoài của tam giác ADB
b. Tính góc EDF