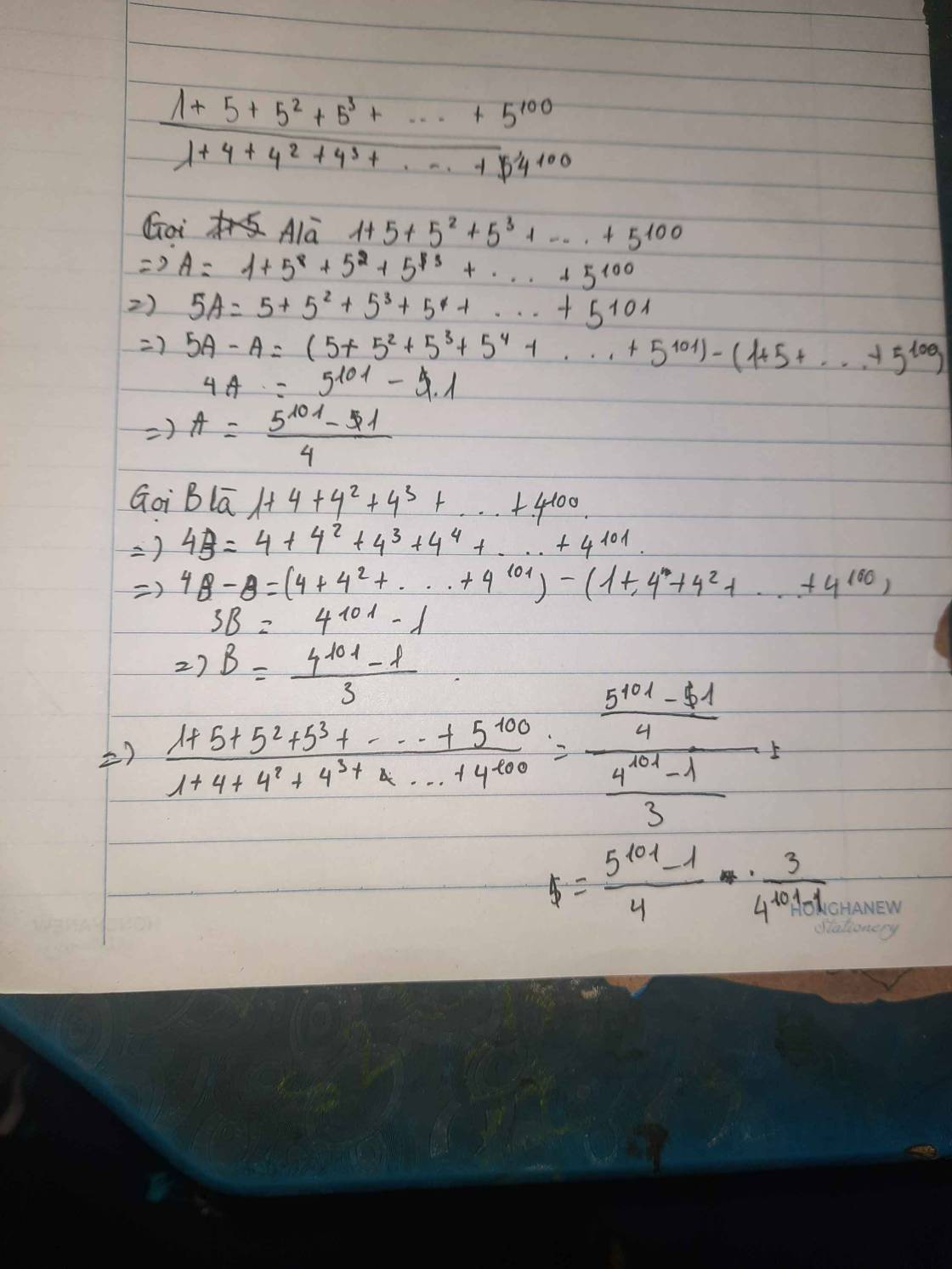100*2/4*5/2

Những câu hỏi liên quan
A=(1^100+2^100+…+10^100).(5^10-25^5)
B=(2^5+3^5+4^5).(1^2+2^2+…+100^2).(4^10-2^20)
bài 1
A=1*2*3+2*3*4+3*4*5+...+99*100*101
B=1*3*5+3*5*7+...+95*97*99
C=2*4+4*6+..+98*100
D=1*2+3*4+5*6+...+99*100
E=1^2+2^2+3^2+...+100^2
G=1*3+2*4+3*5+4*6+...+99*101+100*102
H=1*2^2+2*3^2+3*4^2+...+99*100^2
I=1*2*3+3*4*5+5*6*7+7*8*9+...+98*99*100
K=1^2+3^2+5^2+...+99^2
A = 1*2*3 + 2*3*4 + 3*4*5 ... + 99*100*101
=> 4A = 1*2*3*4 + 2*3*4*4 + 3*4*5*4 + ... +99*100*101*4
=> 4A = 1*2*3*4 + 2*3*4*(5 - 1) + 3*4*5*( 6 - 2) + ... + 99*100*101*(102 - 98)
=> 4A = 1*2*3*4 + 2*3*4*5 - 1*2*3*4 + 3*4*5*6 - 2*3*4*5 + ... + 99*100*101*102 - 98*99*100*101
=> 4A = 99*100*101*102
=> 4A = 101989800
=> A = 25497450
Tính nhanh A = (1^100+2^100+…+10^100).(5^10-25^5)
B = (2^5+3^5+4^5).(1^2+2^2+…+100^2).(4^10-2^20)
Bạn tự hỏi rồi từ trả lời ! Bạn xem đầu bạn có nóng không ?
Đúng 0
Bình luận (0)
`Answer:`
\(A=\left(1^{100}+2^{100}+...+10^{100}\right)\left(5^{10}-25^5\right)\)
\(=\left(1^{100}+2^{100}+...+10^{100}\right)[5^{10}-\left(5^2\right)^5]\)
\(=\left(1^{100}+2^{100}+...+10^{100}\right)\left(5^{10}-5^{10}\right)\)
\(=\left(1^{100}+2^{100}+...+10^{100}\right).0\)
\(=0\)
\(B=\left(2^5+3^5+4^5\right)\left(1^2+2^2+...+100^2\right)\left(4^{10}-2^{20}\right)\)
\(=\left(2^5+3^5+4^5\right)\left(1^2+2^2+...+100^2\right)\left(2^{2.10}-2^{20}\right)\)
\(=\left(2^5+3^5+4^5\right)\left(1^2+2^2+...+100^2\right).0\)
\(=0\)
S=1×2+2×3+3×4+4×5+...........+99×100
3S=1×2×3+2×3×(4-1)+3×4×(5-2)+4×5×(6-3)+............+99×100×(101-98)
3S=1×2×3+2×3×4-1×2×3+3×4×5-2×3×4+4×5×6-3×4×5+.............+99×100×101-98×99×100
3S=99×100×101
Tại sao 3S=99×100×101
Các bạn giải thích hộ mình với!
MÌNH CẢM ƠN MỌI NGƯỜI!
tính nhanh
A=(1^100+2^100+…+10^100).(5^10-25^5)
B=(2^5+3^5+4^5).(1^2+2^2+…+100^2).(4^10-2^20)
Tính C=1/2-(1/3+2/3)+(1/4+2/4+3/4)-(1/5+2/5+3/5+4/5)+...+(1/100+2/100+...+99/100)
S=1×2+2×3+3×4+4×5+...........+99×100
3S=1×2×3+2×3×(4-1)+3×4×(5-2)+4×5×(6-3)+............+99×100×(101-98)
3S=1×2×3+2×3×4-1×2×3+3×4×5-2×3×4+4×5×6-3×4×5+.............+99×100×101-98×99×100
3S=99×100×101
Tại sao 3S=99×100×101
Các bạn giải thích hộ mình với!
MÌNH CẢM ƠN MỌI NGƯỜI!
\(\dfrac{1+5+5^2+5^3+...+5^{100}}{1+4+4^2+4^3+...+4^{100}}\)
1. (1+1/2).(1+1/2^2).(1+1/2^3)....(1+1/2^100) < 3
2. 1/(5+1)+2/(5^2+1)+4/(5^4+1)+...+ 1024/(5^1024+1) <1/4
3. 3/(1!+2!+3!)+4/(2!+3!+4!)+...+100/(98!+99!+100!) <1/2
??????????????????????????????????????????????
Đúng 0
Bình luận (0)
Lần đầu post, mình quên mất chưa nêu câu hỏi. Nhờ các bạn chứng minh dùm 3 câu trên với, cám ơn nhiều ah!
Đúng 0
Bình luận (0)
1.\(\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)+...+\left(1+\frac{1}{2^{100}}\right)\)
Đặt \(A=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{100}}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{99}}\)
\(\Rightarrow2A-A=\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{99}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{100}}\right)\)
\(\Rightarrow A=1-\frac{1}{2^{100}}\)
Thấy:\(\frac{1}{2^{100}}>0\Rightarrow1-\frac{1}{2^{100}}< 1\)
\(\Rightarrow A< 1\)
Ta có:\(\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)...\left(1+\frac{1}{2^{100}}\right)=A+100< 1+100=101\)
\(101>\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)...\left(1+\frac{1}{2^{100}}\right)\ge100\)
\(\Rightarrow\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)...\left(\frac{1}{2^{100}}\right)>\left(\frac{101}{100}\right)^{100}>3\)
*Cách khác:
\(\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)+...+\left(1+\frac{1}{2^{100}}\right)\)
\(=\frac{2+1}{2}.\frac{2^2+1}{2^2}....\frac{2^{100}+1}{2^{100}}\)
Ta thấy:
\(\frac{2+1}{2}>\frac{2^2+1}{2^2}>....>\frac{2^{100}+1}{2^{100}}\)
\(\Rightarrow\frac{2+1}{2}>\frac{2+1}{2}.\frac{2^2+1}{2^2}....\frac{2^{100}+1}{2^{100}}\)
Mà \(\frac{2+1}{2}< 3\)
\(\Rightarrow\frac{2+1}{2}.\frac{2^2+1}{2^2}....\frac{2^{100}+1}{2^{100}}< 3\)
\(\Rightarrow\left(1+\frac{1}{2}\right)\left(1+\frac{1}{2^2}\right)\left(1+\frac{1}{2^3}\right)+...+\left(1+\frac{1}{2^{100}}\right)< 3\)
Xem thêm câu trả lời
tính A= 1+ 3/2^2+4/2^4+5/2^5+.....+100/2^100
A=1+3/2^3+4/2^4+5/2^5+...100/2^100
1/2*A = 1/2 + 3/2^4 + 4/2^5 +....+ 99/2^100 + 100/2^101
A- A/2 = 1/2A =1/2 + 3/2^3 + 1/2^4 +...+1/2^100 - 100/2^101=
= [1/2+1/2^2 +1/2^3 +...+1/2^100] -100/2^101 (Do 3/2^3 = 1/2^2 +1/2^3)
=[1-(1/2)^101]/(1-1/2) -100/2^101 =
=(2^101 -1)/2^100 - 100/2^101
=> A= (2^101 -1)/2^99 - 100/2^100
Đúng 0
Bình luận (0)