Cho hình bình hành ABCD. Một đưòng thẳng song song với AC, cắt AB ở E, cắt BC ở F. c/m diện tích DAE= diện tích DCF

Những câu hỏi liên quan
Cho hình bình hành ABCD. Vẽ một đường thẳng song song AC cắt cạnh AB tại E, cắt cạnh BC ở F. CMR diện tích 2 tam giác DAE và DCF bằng nhau.
Cho hình bình hành ABCD. Một đường thẳng song song với AC, cắt cạnh AB ở E, cắt cạnh BC ở F. Chứng minh SDAE=SDCF
CHO HÌNH BÌNH HÀNH ABCD. MỘT ĐƯỜNG THẲNG SONG SONG VỚI AC, CẮT CẠNH AB Ở E, CẮT CẠNH BC Ở F. CM
SDAE=SDCF
Cho hình bình hành ABCD. Gọi M,N lần lượt là hai điểm trên cạnh BC , CD . Đường chéo BD cắt AM,AN theo thứ tự ở E và F . Các đường thẳng qua E song song với BC , qua F song song với AD cắt nhau ở I
a) chứng minh Diên tích tam giác AEF = Diện tích tam giác IDB
b) Giả sử Diện tích tam giác AEF = Diện tích tứ giác EMNF,chứng minh 3 điểm M,I,N thẳng hàng
Cho hình bình hành ABCD. Gọi M,N lần lượt là hai điểm trên cạnh BC , CD . Đường chéo BD cắt AM,AN theo thứ tự ở E và F . Các đường thẳng qua E song song với BC , qua F song song với AD cắt nhau ở I
a) chứng minh Diên tích tam giác AEF = Diện tích tam giác IDB
b) Giả sử Diện tích tam giác AEF = Diện tích tứ giác EMNF,chứng minh 3 điểm M,I,N thẳng hàng
ko biết
Cho hình bình hành ABCD. Vẽ đường thẳng song song với AC cắt AB tại M, cắt BC tại N. Chứng minh: diện tích ADM = diện tích CDN.
Vì MN // AC nên
\(\Rightarrow\frac{MA}{BA}=\frac{NC}{BC}\Rightarrow MA.BC=NC.BA\)
\(\Rightarrow MA.AD=NC.DC\)
\(\Rightarrow\frac{1}{2}.MA.AD.\sin\left(\widehat{MAD}\right)=\frac{1}{2}.NC.DC.\sin\left(\widehat{MAD}\right)\)
\(\Rightarrow\Rightarrow\frac{1}{2}.MA.AD.\sin\left(\widehat{MAD}\right)=\frac{1}{2}.NC.DC.\sin\left(\widehat{NCD}\right)\)
\(\Rightarrow S_{ADM}=S_{CDN}\)
Đúng 0
Bình luận (0)
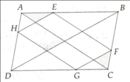
Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.

Áp dụng định lý Thalès, ta có:
HE // BD \(\Rightarrow\frac{AH}{AD}=\frac{AE}{AB}\)(1)
EF // AC \(\Rightarrow\frac{AE}{AB}=\frac{FC}{BC}\)(2)
FG // BD \(\Rightarrow\frac{FC}{BC}=\frac{GC}{DC}\)(3)
Từ (1),(2),(3) suy ra \(\frac{AH}{AD}=\frac{GC}{DC}\Rightarrow AH.CD=AD.CG\left(đpcm\right)\)
Cho hình bình hành ABCD. Gọi E là một điểm bất kỳ trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ qua F song song với BD cắt CD ở G. Chứng minh A H . C D = A D . C G .
Cho hình bình hành ABCD, đường thẳng d song song với AC và cắt AB, BC lần lượt tại M, N.
So sánh diện tích tam giác ADM và diện tích tam giác CDN.