sd

Những câu hỏi liên quan
Giúp mik câu này với : Vẽ sơ đồ nguyên lí mạch điện theo yêu cầu gồm : Đèn D1 sd UAB xoay chiều , đèn D2 sd 2UAB xoay chiều , đèn D3 sd UAB chỉnh lưu 1 nửa chu kì , đèn D4 sd UAB chỉnh lưu 2 nửa chu kì
Lập dàn ý cho đề bài :"sự bổ ích của những chuyến tham quan,du lịch đối với học sinh" có sd luận điểm,luận cứ sd yếu tố biểu cảm và sd nghệ thuật
- Mở bài: Giới thiệu vấn đề nghị luận.
- Thân bài:
+ Lợi ích tham quan du lịch:
. Đem đến cảm giác thoải mái sau những ngày làm việc căng thẳng (tránh xa mọi áp lực công việc, hòa mình vào thiên nhiên, phục hồi sức khỏe,…)
. Cơ hội để mở rộng tầm nhìn, hiểu biết về cuộc sống (tích lũy tri thức là một cách học hết sức hiệu quả, trưởng thành trong nhận thức, ứng xử,…)
. Cơ hội giao lưu, kết bạn.
+ Tham quan du lịch như thế nào cho hữu ích:
. Có tổ chức, kế hoạch cụ thể, tránh tùy hứng thiếu chủ động.
. Tùy điều kiện hoàn cảnh bản thân để có kế hoạch phù hợp.
- Kết bài: Tham quan du lịch là một hình thức tiêu khiển, học tập bổ ích, thú vị. Hãy tổ chức cuộc sống một cách khoa học để thực hiện những chuyến tham quan hữu ích.
Đúng 0
Bình luận (0)
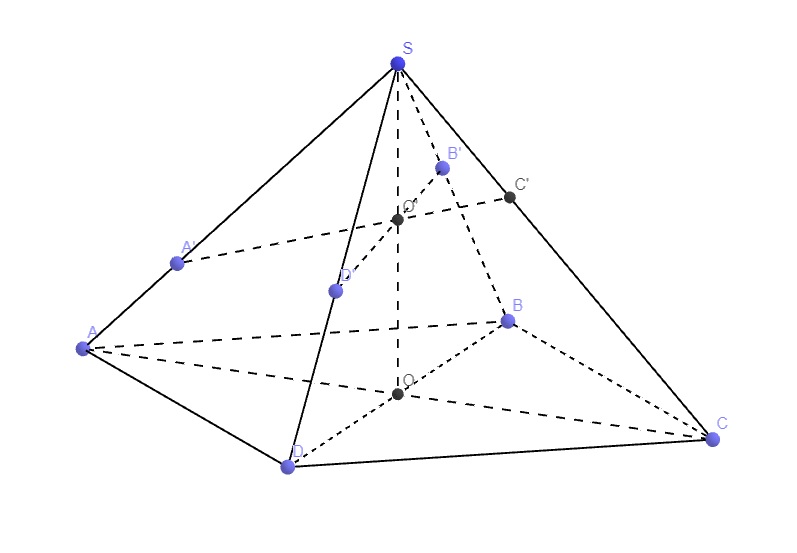
Cho hinh chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng \(\left(\alpha\right)\) cắt SA, SB, SC, SD tại A', B', C', D'. CMR: \(\dfrac{SA}{SA'}+\dfrac{SB}{SB'}=\dfrac{SC}{SC'}+\dfrac{SD}{SD'}\)
Cho đường tròn tâm ( O ) đường kính AB góc nội tiếp ADC=160° CM là tiếp tuyến của đường tròn ( O ) tại C
a. tính sd góc AOC
b. Tính sd góc ACM
c. Tính sd góc ACB
Ai giúp mình với ạ
Xem chi tiết
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)\)
Trước hết ta chứng minh 1 bổ đề đơn giản về diện tích tam giác như sau (em tự vẽ hình)
Cho tam giác ABC, trên các cạnh AB và AC lần lượt lấy 2 điểm B' và C', khi đó ta có:
\(\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{AB'.AC'}{AB.AC}\)
Chứng mình: từ C và C' lần lượt hạ CH và C'H' vuông góc AB, khi đó CH song song C'H' nên theo Talet:
\(\dfrac{C'H'}{CH}=\dfrac{AC'}{AC}\)
\(\Rightarrow\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{\dfrac{1}{2}C'H'.AB'}{\dfrac{1}{2}CH.AB}=\dfrac{AC'.AB'}{AC.AB}\)
Quay lại bài, gọi O là tâm đáy
Trong mp (SAC), tại O' là giao điểm của SO và A'C'
Ba mặt phẳng (SAC), (SBD), \(\left(\alpha\right)\) cắt nhau theo 3 giao tuyến phân biệt là SO, A'C', B'D' nên 3 giao tuyến này song song hoặc đồng quy.
Mà SO và A'C' cắt nhau tại O' nên 3 đường thẳng nói trên đồng quy tại O'
Ta có:
\(S_{SA'C'}=S_{SA'O'}+S_{SC'O'}\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{S_{SAC}}+\dfrac{S_{SC'O'}}{S_{SAC}}\)
\(\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{2S_{SAO}}+\dfrac{S_{SC'O'}}{S_{SCO}}\Rightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SA'.SO'}{2SA.SO}+\dfrac{SC'.SO'}{2SC.SO}\)
\(\Leftrightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SO'}{2SO}\left(\dfrac{SA'}{SA}+\dfrac{SC'}{SC}\right)\)
\(\Leftrightarrow SA'.SC'=\dfrac{SO'}{2SO}\left(SC.SA'+SA.SC'\right)\)
\(\Leftrightarrow1=\dfrac{SO'}{2SO}\left(\dfrac{SC}{SC'}+\dfrac{SA}{SA'}\right)\)
\(\Leftrightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}=\dfrac{2SO}{SO'}\)
Hoàn toàn tương tự, ta cũng có \(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}=\dfrac{2SO}{SO'}\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)=0\)
Đúng 2
Bình luận (0)
Cho (O;R) lần lượt đặt theo cùng một chiều kể từ A, ba cung AB,BC, CD, sd AB=60 độ, sd cung BC=90 độ, sd cung DC =120 độ. Gọi S là giao điểm của AC và DB. TÍnh tỉ số SA/SC
cho chóp SABCD đáy hình bình hành M là trung điểm SC , mặt anpha chứa AM cắt SD,SB tại E;F tính SD/SE
Đề thiếu dữ liệu rồi em, mp \(\left(\alpha\right)\) chỉ có tính chất chứa AM thì ko thể tính được tỉ số SD/SE (có vô số giá trị thỏa mãn)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có SA⊥(ABCD)SA⊥(ABCD)và đáy ABCD là hình vuông. Gọi H,K là hình chiếu của A lên SB,SD
a) Cm AH⊥(SBC)
b) Cm AK⊥(SCD)
c) Qua K vẽ đường thẳng vuông góc với SD tại K cắt CD tại M. Cm SD⊥(BKM)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi G là trọng tâm tam giác SAC. Mặt phẳng (a) qua G cắt SA; SB; SC; SD lần lượt tại A'B'C'D'.
1) Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}-\dfrac{SD}{SD'}\right)\)
2 ) Tính \(\dfrac{SA}{SA'}+\dfrac{SB}{SB'}+\dfrac{SC}{SC'}+\dfrac{SD}{SD'}\)
tìm số dư và thương trong phép chia biết sbc là 49 và sd là11
tìm sc và sd trong phép chia biết sbc là 36 và thương là 7
trong 1 pc có sbc là 155 sd là 12 tìm sc và thương
1.có số dư r
2.sc=5 sd = 1
3.gợi ý: thương x số chia (= 155-12)=143
Đúng 0
Bình luận (0)