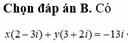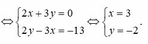tìm các số nguyên dương x,y,z thoả mãn x2 + y3+z4=90

Những câu hỏi liên quan
tìm các số x ,y, z biết (-x2.y3)2+(2.y2.z4)3=0
Lời giải:
Ta thấy:
$(-x^2y^3)^2\geq 0$ với mọi $x,y$
$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$
$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:
$-x^2y^3=2y^2z^4=0$
Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.
Đúng 0
Bình luận (0)
Tìm tất cả các số nguyên dương \(x;y;z\) thoả mãn : \(3^x+2^y=1+2^z\)
Tìm các số thực dương x,y,z thoả mãn:
x. căn của (1-y2) + y. căn của (2-z2) + z. căn của (3-x2) = 3
Tìm các số thực x, y thoả mãn
x
2
-
3
i
+
y
3
+
2
i
-
13
i
với i là đơn vị ảo.
Đọc tiếp
Tìm các số thực x, y thoả mãn x 2 - 3 i + y 3 + 2 i = - 13 i với i là đơn vị ảo.
![]()
![]()
![]()
![]()
Tìm tất cả các bộ số nguyên dương (x;y;z) thoả mãn \(\dfrac{x}{y}=\dfrac{y+x}{y+z}\) và
(y + 2).(4xz + 6y - 3) là số chính phương.
\(\dfrac{x}{y}=\dfrac{x+y}{y+z}=\dfrac{y}{z}\Rightarrow xz=y^2\)
\(\left(y+2\right)\left(4xz+6y-3\right)=n^2\)
\(\Rightarrow\left(y+2\right)\left(4y^2+6y-3\right)=n^2\)
Gọi \(d=ƯC\left(y+2;4y^2+6y-3\right)\)
\(\Rightarrow4y^2+6y-3-\left(y+2\right)\left(4y-2\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow y+2\) và \(4y^2+6y-3\) nguyên tố cùng nhau
Mà \(\left(y+2\right)\left(4y^2+6y-3\right)\) là SCP \(\Rightarrow y+2\) và \(4y^2+6y-3\) đồng thời là SCP
\(\Rightarrow4y^2+6y-3=k^2\)
\(\Leftrightarrow\left(4y+3\right)^2-21=\left(2k\right)^2\)
\(\Rightarrow\left(4y+3-2k\right)\left(4y+3+2k\right)=21\)
Giải pt ước số trên ra \(y=2\) là số nguyên dương duy nhất thỏa mãn
Thế vào \(xz=y^2=4\Rightarrow\left(x;z\right)=\left(1;4\right);\left(4;1\right);\left(2;2\right)\)
Vậy \(\left(x;y;z\right)=\left(1;2;4\right);\left(4;2;1\right);\left(2;2;2\right)\)
Đúng 1
Bình luận (0)
Tìm các số nguyên x, y, z đồng thời thoả mãn các điều kiện sau :
x2 = y - 1 ; y2 = z -1 ; z2 = x - 1
Tìm các số nguyên dương x,y,z thoả mãn: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
tham khảo https://olm.vn/hoi-dap/detail/2037215608.html
#Học-tốt
Ta có : \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
=> \(\frac{xy+yz+xz}{xyz}=1\)
=> xy + yz + xz - xyz = 0 (1)
=> y(x + z) + xy(1 - z) = 0
=> y[x + z + (1 - z).x] = 0
=> \(\orbr{\begin{cases}y=0\left(\text{loại}\right)\\x+z+x\left(1-z\right)=0\end{cases}\Rightarrow x\left(2-z\right)+z=0\Rightarrow\left(x-1\right)\left(2-z\right)=-2}\)
Lại có \(x;z\inℕ^∗\Rightarrow\hept{\begin{cases}x-1\inℕ^∗\Leftrightarrow x>1\\2-z\inℕ^∗\Leftrightarrow z< 2\end{cases}}\)(2)
Từ (1) ta có : -2 = (-2).1 = (-1).2
Lập bảng xét các trường hợp
| x - 1 | -1 | 2 | 1 | -2 |
| 2 - z | 2 | -1 | -2 | 1 |
| x | 0(loại) | 3 | 2 | -3(loại) |
| z | 0(loại) | 3 | 4 | 3 |
| y | \(y\in\varnothing\) | 3 | 2 | 1(loại) |
Vậy các cặp (x;y;z) thỏa mãn là : (3;3;3) ; (2;4;2) ; (2;2;4) ; (4;2;2)
Bỏ phần : "Lại có : \(x;z\inℕ^∗\Rightarrow\hept{\begin{cases}x-1\inℕ^∗\\2-z\inℕ^∗\end{cases}\Leftrightarrow\hept{\begin{cases}x>1\\z< 2\end{cases}}}\)"
Phần đó ghi sai nha !
Tìm các số nguyên dương x,y,z thỏa mãn x^2 + y^3 + z^4 = 90
Vì x, y, z là các số nguyên dương nên x,y,z \(\ge1\)
Ta có
\(x^2+y^3+z^4=90\)
\(\Rightarrow z^4< 90\)
Ta thấy rằng \(\hept{\begin{cases}4^4=256>90\\3^4=81< 90\end{cases}}\)nên z không thể lớn hơn 4 được
Hay z nhận các giá trị là 1, 2, 3
Với z = 3 thì
\(x^2+y^3=90-3^4=9\)
Tương tự như trên ta cũng thấy được: y chỉ thể nhận các giá trị 1,2
Thế vô lần lược tìm được: y = 2, x = 1
Xét lần lược các trường hợp của z sẽ tìm được các nghiêm còn lại
Các bộ số cần tìm là: \(\left(x,y,z\right)=\left(1,2,3\right);\left(5,4,1\right);\left(9,2,1\right)\)
Mình chỉ hướng dẫn bạn cách làm thôi nhé.
Đúng 0
Bình luận (0)
Vì x,y,z là các số nguyên dg nên x,y,z >/1
Ta có : x2 +y3 +z4 = 90
Suy ra z4 < 90
Ta thấy rằng {42 = 256 > 90 , 34 = 81 < 90 nên z ko thể >4
Hay z nhận các gt là 1,2,3
Với z=3 thì :
x2
Tìm các số nguyên dương x,y,z thỏa mãn x^2+y^3+z^4=90.