Sử dụng phương pháp "dãy số viết theo quy luật" hãy chứng minh: 1414-1 chia hết cho 3.

Những câu hỏi liên quan
Bài 3:
Cho dãy số viết theo quy luật: \(1\frac{1}{2};1\frac{1}{5};1\frac{1}{9};1\frac{1}{14};1\frac{1}{20};...\) (1)
a) Hãy viết tiếp vào chỗ ... số thứ sáu theo quy luật của dãy.
b)Tìm số thứ 50 của dãy (1)
c) Chứng minh rằng tích 50 số đầu tiên của dãy nhỏ hơn 3.
Sử dụng phương pháp đồng dư thức hãy chứng minh:
a) 1414 chia hết cho 3.
b) 20092009 chia hết cho 2008.
Sử dụng phương pháp đồng dư thức hãy chứng minh:
a) 1414 chia hết cho 3.
b) 20092009 chia hết cho 2008.
Cho dãy số được viết theo quy luật: -19; -15; -11; -7. Hãy chỉ ra quy luật và viết ba số tiếp theo của dãy
Quy luật là: số liền sau bằng số liền trước cộng với 4.
Viết ba số tiếp theo của dãy là: -3; 1; 5
Đúng 0
Bình luận (0)
Cho dãy số
u
n
, biết
u
1
-
1
,
u
n
+
1
u
n
+
3
v
ớ
i
n
≥...
Đọc tiếp
Cho dãy số u n , biết u 1 = - 1 , u n + 1 = u n + 3 v ớ i n ≥ 1 .
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: u n = 3 n – 4
a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.
Đúng 0
Bình luận (0)
Cho dãy số 1,1,2,3,7,22,... với quy luật là mỗi số hạng kể từ số thứ 3 bằng tích của hai số hạng đứng trước nó cộng với 1. Chứng minh rằng: Các số chẵn của dãy số thì không chia hết cho 4
Biết bốn số hạng đầu của một dãy số là -1, 3, 7, 11.
Từ đó hãy chỉ ra một quy luật rồi viết tiếp năm số hạng của dãy theo quy luật đó.
Ta có
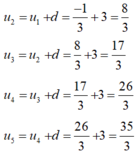
Quy luật: kể từ số thứ 2, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 4. Năm số hạng tiếp của dãy theo quy luật đó: 15; 19; 23; 27; 31
Đúng 0
Bình luận (0)
Dãy số
u
n
cho bởi
u
1
3
,
u
n
+
1
1
+
u
n
2
,
n
1...
Đọc tiếp
Dãy số u n cho bởi u 1 = 3 , u n + 1 = 1 + u n 2 , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
a. Năm số hạng đầu của dãy số
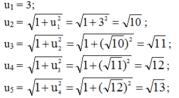
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
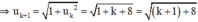
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
Đúng 0
Bình luận (0)
Bài 1: Cho các dãy phân sô: 2007/2006, 2008/2007,2009/2008,2010/2009
a. Hãy viết tiếp số hạng thứ 5 vào dãy số trên theo đúng quy luật.
b. Chứng tỏ rằng dãy trên là một dãy xếp theo thứ tự tăng dần







