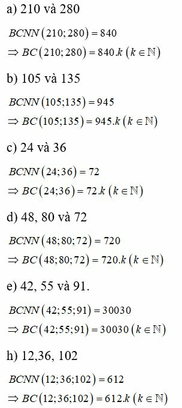Hãy tìm bội chung của (10, 18, 24 ) thông qua bội chung nhỏ nhất

Những câu hỏi liên quan
bài 8a)Tìm các bội chung của 7;9;6 thông qua tìm BCNN (Bội Chung Nhỏ Nhất)b)Tìm các bội chung của 8;12;15 thông qua tìm BCNNBài 9 Tìm BCNN củaa) 15;18 e) 33;44;55b) 8;18;30 f) 10;12c) 4;14;26 g) 24;10d) 6;8;10 ...
Đọc tiếp
bài 8
a)Tìm các bội chung của 7;9;6 thông qua tìm BCNN (Bội Chung Nhỏ Nhất)
b)Tìm các bội chung của 8;12;15 thông qua tìm BCNN
Bài 9 Tìm BCNN của
a) 15;18 e) 33;44;55
b) 8;18;30 f) 10;12
c) 4;14;26 g) 24;10
d) 6;8;10 h) 84;108
Mình cảm ơn!
`8)`
`a)` `->` ta được BCNN `(7;9;6)=126`
`->` từ đó ta có được BC `(7;9;6)={0;126;252;...}`
`b)` `->` ta được BCNN `(8;12;15)=120`
`->` từ đó ta được BC `(8;12;15)={0;120;240;...}`
`9)`
`a)->` BCNN `(15;18)=90`
`e)->` BCNN`(33;44;55)=660`
`b)->` BCNN`(8;18;30)=360`
`f)->` BCNN`(10;12)=60`
`c)->` BCNN `(4;14;26)=364`
`g)->` BCNN `(24;10)=210`
`d)->` BCNN `(6;8;10)=120`
Đúng 2
Bình luận (0)
2 bài này khá dài khi giải ra nên mik chỉ giảng cách tính thôi:
Bước 1: Phân tích từng số ra tích các thừa số nguyên tố.
Bước 2: Tìm BCNN bằng cách nhân các thừa số nguyên tố với nhau với số mũ lớn nhất (nếu có chung)
Đúng 1
Bình luận (0)
Nêu khái niệm về:
1. Ước và Bội.
2. Cách tìm bội
3. Cách tìm ước.
4. Số nguyên tố.
5. Ước chung.
6. Ước chung lớn nhất - ƯCLN
7. Cách tìm ước chung lớn nhất - ƯCLN
8. Cách tìm ƯớC thông qua UCLN.
9. Bội chung.
10. Các tìm bội chung nhỏ nhất. (BCNN)
11. Cách tìm bội chung thông qua BCNN.
1)a chia hết cho b thì b là ước của a
a chia hết cho b thì b là bội của a.
2)Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
3)Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
4)Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
5)Ước chung của hai hay nhiều số là ước của tất cả các số đó.
6) Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
7)ƯCLN của hai hay nhiều số là số lơn nhất trong tập hợp ước chung
9)Bội chung của hai hay nhiều số là bội của tất cả các số đó.
10

Đúng 0
Bình luận (0)
1)a chia hết cho b thì b là ước của a
a chia hết cho b thì b là bội của a.
2)Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
3)Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
4)Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
5)Ước chung của hai hay nhiều số là ước của tất cả các số đó.
6) Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
- Bước 2: Chọn ra các thừa số nguyên tố chung.
- Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.
7)ƯCLN của hai hay nhiều số là số lơn nhất trong tập hợp ước chung
9)Bội chung của hai hay nhiều số là bội của tất cả các số đó.
10

Đúng 0
Bình luận (0)
cách tìm bội chung thông qua tìm bội chung nhỏ nhất
Tìm bội chung thông qua bội chung nhỏ nhấta) 210 và 280 b) 105 và 135 c) 24 và 36f) 48, 80 và 72 g) 42, 55 và 91. h)12, 36, 102
Đọc tiếp
Tìm bội chung thông qua bội chung nhỏ nhất
a) 210 và 280
b) 105 và 135
c) 24 và 36
f) 48, 80 và 72
g) 42, 55 và 91.
h)12, 36, 102
Tìm bội chung thông qua bội chung nhỏ nhất:
a, 210 và 280
b, 105 và 135
c, 24 và 36
d, 48, 80 và 72
e, 42, 55 và 91
f, 12,36 và 102
a, BCNN(210;280) = 840 => BC(210;280) = 840k (k ∈ N)
b, BCNN(105;135) = 945 => BC(105;135) = 945k (k ∈ N)
c, BCNN(24;36) = 72 => BC(24;36) = 72k (k ∈ N)
d, BCNN(48;80;72) = 720 => BC(48;80;72) = 720k (k ∈ N)
e, BCNN(42;55;91) = 30030 => BC(42;55;91) = 30030k (k ∈ N)
f, BCNN(12;36;102) = 612 => BC(12;36;102) = 612k (k ∈ N)
Đúng 0
Bình luận (0)
tìm bội chung nhỏ nhất của 10 12 18
tham khảo
Bội chung nhỏ nhất của 10, 12, 18 và 5 là 180.
Đúng 1
Bình luận (4)
Bội chung nhỏ nhất của 10, 12, 18 và 5 là 180.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
tìm bội chung nhỏ nhất rồi tìm bội chung của :(12 , 15 và 24 )
Ta có:
\(12=2^2.3\)
\(15=3.5\)
\(24=2^3.3\)
\(BCNN\left(12;15;24\right)=2^3.3.5=8.3.5=120\)
\(BC\left(12;15;24\right)=B\left(120\right)=\left\{0;120;240;360;480;...\right\}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a) Tìm BC của 8 và 10b) Tìm BC của 6; 24 và 40c) Tìm BC của 8; 15 và 20.d) Tìm các bội chung nhỏ hơn 500 của 30 và 45.e)Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng
a
⋮
15
và
a
⋮
18
. f) Tìm các bội chung có ba chữ số của
63
;
35
;
105
.
Đọc tiếp
a) Tìm BC của 8 và 10
b) Tìm BC của 6; 24 và 40
c) Tìm BC của 8; 15 và 20.
d) Tìm các bội chung nhỏ hơn 500 của 30 và 45.
e)Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18 .
f) Tìm các bội chung có ba chữ số của 63 ; 35 ; 105 .
a)Tìm BC của 8 và 10b) Tìm BC của 6; 24 và 40c) Tìm BC của 8; 15 và 20.d) Tìm các bội chung nhỏ hơn 500 của 30 và 45.e)Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a
⋮
15 và a
⋮
18.f) Tìm các bội chung có ba chữ số của 63;35;105
Đọc tiếp
a)Tìm BC của 8 và 10
b) Tìm BC của 6; 24 và 40
c) Tìm BC của 8; 15 và 20.
d) Tìm các bội chung nhỏ hơn 500 của 30 và 45.
e)Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18.
f) Tìm các bội chung có ba chữ số của 63;35;105
a, Ta có: 8 = 2 3 ; 10 = 2.5
BCNN(8; 10) = 2 3 .5 = 40
BC(8; 10) =B(40)= { 0; 40; 80; 120;………}
b, Ta có: 6 =2.3; 24= 2 3 . 3; 40 = 2 3 .5
BCNN( 6; 24; 40) = 2 3 .3. 5= 120
BC( 6; 24; 40)= B(120) ={ 0; 120; 240; 360….}
c, Ta có: 8 = 2 3 ; 15 = 3.5; 20 = 2 2 .5
BCNN(8; 15;20) = 2 3 .3.5 = 120
BC( 8; 15; 20)= B(120) ={ 0; 120; 240; 360….}
d, Ta có: 30 = 2.3.5; 45 = 3 2 .5
BCNN(30; 45) = 2. 3 2 .5 = 90
BC (30; 45) và nhỏ hơn 500 = { 0; 90; 180; 270; 360;480}
e, Ta có: a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18
=> a = BCNN (15; 18)
Có: 15 = 3.5; 18 = 2. 3 2
BCNN(15; 18) = 2. 3 2 .5 = 90
Vậy a = 90
f, Ta có: 63 = 3 2 .7; 35 = 5.7; 105 = 3.5.7
BCNN(63; 35; 105) = 3 2 .5.7 = 315
BC(63; 35; 105) và nhỏ hơn 1000 = { 0; 315; 630; 945}
Đúng 0
Bình luận (0)
a, Ta có: 8 = 2 3 ; 10 = 2.5
BCNN(8; 10) = 2 3 .5 = 40
BC(8; 10) =B(40)= { 0; 40; 80; 120;………}
b, Ta có: 6 =2.3; 24= 2 3 . 3; 40 = 2 3 .5
BCNN( 6; 24; 40) = 2 3 .3. 5= 120
BC( 6; 24; 40)= B(120) ={ 0; 120; 240; 360….}
c, Ta có: 8 = 2 3 ; 15 = 3.5; 20 = 2 2 .5
BCNN(8; 15;20) = 2 3 .3.5 = 120
BC( 8; 15; 20)= B(120) ={ 0; 120; 240; 360….}
d, Ta có: 30 = 2.3.5; 45 = 3 2 .5
BCNN(30; 45) = 2. 3 2 .5 = 90
BC (30; 45) và nhỏ hơn 500 = { 0; 90; 180; 270; 360;480}
e, Ta có: a nhỏ nhất khác 0, biết rằng a ⋮ 15 và a ⋮ 18
=> a = BCNN (15; 18)
Có: 15 = 3.5; 18 = 2. 3 2
BCNN(15; 18) = 2. 3 2 .5 = 90
Vậy a = 90
f, Ta có: 63 = 3 2 .7; 35 = 5.7; 105 = 3.5.7
BCNN(63; 35; 105) = 3 2 .5.7 = 315
BC(63; 35; 105) và nhỏ hơn 1000 = { 0; 315; 630; 945}
Đúng 0
Bình luận (0)