máy vi tính vào giai đoạn đầu được dùng cho

Những câu hỏi liên quan
Hãy liệt kê tất cả các giai đoạn xử lí tín hiệu theo thứ tự từ đầu vào đến đầu ra của các máy sau đây :
Máy phát sóng vô tuyến.
Trong mỗi giai đoạn, hãy nêu : tên của bộ phận máy dùng trong việc xử lí; chức năng của bộ phận đó ; kết quả của việc xử lí.
Máy phát sóng vô tuyến
Giai đoạn 1 : Biến đổi dao động âm thành dao động điện có cùng tần sò. Dùng micrô để thực hiện sự biến đổi này. Kết quả, ta được dao động điện có tần số âm (dao động âm tần).
Giai đoạn 2 : Biến điệu dao động (sóng) điện từ cao tần, tức là làm ch dao động cao tần tải được các tín hiệu âm tần. Trong việc biến điệu biên độ, ta làm cho biên độ của dao động cao tần biến đổi theo tần số âm.
Dùng một mạch phát dao động điện từ cao tần để tạo ra dao động điện từ cao tần. Dao động điện từ cao tần được trộn với dao động điện từ âm tần trong mạch biến điệu.
Kết quả ta được dao động điện từ cao tần biến điệu.
Giai đoạn 3 : Khuếch đại dao động điện từ cao tần bằng một mạch khuếch đại. Kết quả ta được một dao động điện từ cao tần biến điệu có biên độ lớn.
Giai đoạn 4 : Phát sóng. Dao động điện từ cao tần biến điệu, sau khi đã được khuếch đại, được anten phát. Từ đó, có một sóng điện từ cao tần lan truyền đi trong không gian.
Đúng 0
Bình luận (0)
Hãy liệt kê tất cả các giai đoạn xử lí tín hiệu theo thứ tự từ đầu vào đến đầu ra của các máy sau đây :
Máy thu thanh đơn giản.
Trong mỗi giai đoạn, hãy nêu : tên của bộ phận máy dùng trong việc xử lí; chức năng của bộ phận đó ; kết quả của việc xử lí.
Máy thu thanh đơn giản
Giai đoạn 1 : Thu sóng. Dùng một anten thu kết nối với một mạch dao động ở lối vào của máy thu thanh. Mạch dao động được điều chỉnh ở chế độ cộng hưởng. Sóng điện từ tạo ra một dao động điện từ cộng hưởng trong anten.
Giai đoạn 2 : Khuếch đại cao tần. Dùng một mạch khuếch đại để khuếch đại dao động điện từ cao tần biến điệu thu được ở anten.
Giai đoạn 3 : Tách sóng, tức là tách dao động điện từ âm tần ra khỏi dao động điện từ cao tần. Dùng mạch tách sóng để làm công việc này. Sau mạch tách sóng ta được một dao động điện từ âm tần.
Giai đoạn 4 : Khuếch đại âm tần bằng mạch khuếch đại.
Giai đoạn 5 : Biến đổi dao động điện thành dao động âm. Dao động điện từ âm tần được đưa ra loa. Dòng điện xoay chiểu tần số âm là do màng loa dao động và phát ra âm có cùng tần số.
Đúng 0
Bình luận (0)
Hai bên tham chiến đều đưa ra những phương tiện chiến tranh mới như xe tăng, sử dụng máy bay để trinh sát và ném bom, thậm chí dùng cả hơi độc,... là vào thời điểm nào trong giai đoạn đầu của cuộc Chiến tranh thế giới thứ nhất?
A. Năm 1914
B. Năm 1915
C. Năm 1916
D. Năm 1917
Nối cột A với B sao cho được câu đúng nghĩa?
A
B
Thân máy tính
Có nhiều phím. Khi gõ các phím ta gửi tín hiệu vào máy tính
Màn hình máy tính
dùng để điều khiển máy tính thuận tiện và dễ dàng.
Bàn phím máy tính
là hộp chứa nhiều chi tiết tinh vi, trong đó có bộ xử lí của máy tính.
Chuột máy tính
là nơi hiển thị kết quả làm việc của máy tính
Đọc tiếp
Nối cột A với B sao cho được câu đúng nghĩa?
| A | B | |
|---|---|---|
| Thân máy tính | Có nhiều phím. Khi gõ các phím ta gửi tín hiệu vào máy tính | |
| Màn hình máy tính | dùng để điều khiển máy tính thuận tiện và dễ dàng. | |
| Bàn phím máy tính | là hộp chứa nhiều chi tiết tinh vi, trong đó có bộ xử lí của máy tính. | |
| Chuột máy tính | là nơi hiển thị kết quả làm việc của máy tính |
Mỗi phép nối đúng được
| A | B |
|---|---|
| Thân máy tính | là hộp chứa nhiều chi tiết tinh vi, trong đó có bộ xử lí của máy tính. |
| Màn hình máy tính | là nơi hiển thị kết quả làm việc của máy tính |
| Bàn phím máy tính | Có nhiều phím. Khi gõ các phím ta gửi tín hiệu vào máy tính |
| Chuột máy tính | dùng để điều khiển máy tính thuận tiện và dễ dàng. |
Đúng 0
Bình luận (0)
| A | B |
|---|---|
| Thân máy tính | là hộp chứa nhiều chi tiết tinh vi, trong đó có bộ xử lí của máy tính. |
| Màn hình máy tính | là nơi hiển thị kết quả làm việc của máy tính |
| Bàn phím máy tính | Có nhiều phím. Khi gõ các phím ta gửi tín hiệu vào máy tính |
| Chuột máy tính | dùng để điều khiển máy tính thuận tiện và dễ dàng. |
Đúng 0
Bình luận (0)
Một người đi xe máy chuyển động theo 3 giai đoạn: giai đoạn 1 chuyển động thẳng đều với v1= 12km/h trong 2 km/h đầu tiên; giai đoạn 2 chuyển động vs v2=20km/h trong 30' ; giai đoạn 3 chuyển động trên 4km trong 10' . Tính vận tốc trung bình trên cả đoạn đường.
\(t_1=\frac{S_1}{v_1}=\frac{1}{6}\)
\(S_2=v_2.t_2=10km\)
\(S=S_1+S_2+S_3=16km\)
\(t=t_1+t_2+t_3=\frac{5}{6}h\)
\(\Rightarrow v_{tb}=\frac{S}{t}=19,2\) km/h
Đúng 0
Bình luận (0)
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với
v
1
30
k
m
/
h
trong 10km đầu tiên; giai đoạn 2 chuyển động với
v
2
40
k
m
/
h
trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận...
Đọc tiếp
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với v 1 = 30 k m / h trong 10km đầu tiên; giai đoạn 2 chuyển động với v 2 = 40 k m / h trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận tốc trung bình trên cả đoạn đường.
A. 31km/h
B. 32km/h
C. 33km/h
D. 34km/h
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với
v
1
30
k
m
/
h
trong 10km đầu tiên; giai đoạn 2 chuyển động với
v
2
40
k
m
/
h
trong 3...
Đọc tiếp
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với v 1 = 30 k m / h trong 10km đầu tiên; giai đoạn 2 chuyển động với v 2 = 40 k m / h trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận tốc trung bình trên cả đoạn đường.
Giải:
Thời gian xe máy chuyển động giai đoạn đầu t 1 = S 1 v 1 = 10 30 = 1 3 h
Quãng đường giai đoạn hai chuyển động S 2 = v 2 t 2 = 40. 1 2 = 20 k m
Tổng quãng đường và thời gian vật chuyển động
S = S 1 + S 2 + S 3 = 10 + 20 + 4 = 34 k m
t = t 1 + t 2 + t 3 = 1 3 + 1 2 + 1 6 = 1 h
⇒ v t b = S t = 34 1 = 34 k m / h
Đúng 0
Bình luận (0)
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với
v
1
30
k
m
/
h
trong 10km đầu tiên; giai đoạn 2 chuyển động với
v
2
40km/h trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận tốc trung bình trên cả đoạn đường
Đọc tiếp
Một người đi xe máy chuyển động theo 3 giai đoạn: Giai đoạn 1 chuyển động thẳng đều với v 1 = 30 k m / h trong 10km đầu tiên; giai đoạn 2 chuyển động với v 2 = 40km/h trong 30 phút; giai đoạn 3 chuyển động trên 4km trong 10 phút. Tính vận tốc trung bình trên cả đoạn đường
Thời gian xe máy chuyển động giai đoạn đầu
![]()
Quãng đường giai đoạn hai chuyển động
![]()
Tổng quãng đường và thời gian vật chuyển động
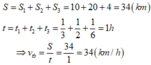
Đúng 0
Bình luận (0)
Thang máy bắt đầu đi lên theo 3 giai đoạn : Giai đoạn 1: Nhanh dần đều không tốc độ đầu, với gia tốc 2m/s2 trong 1s Giai đoạn 2 : thẳng đều trong 5s Giai đoạn 3 : Chậm dần đều cho đến khi dừng lại hết 2s Tìm: a. Tốc độ của chuyển động thẳng đều? b. Quãng đường tổng cộng mà thang máy đi được?
a) v1 = v01 + a1 . t = 2t
t1 = 1 (s) => v2 = v1 = 2 . 1 = 2(m/s)
b) s1 = v01 . t + 1/2 . a1 . t^2 = 0 . 1 + 1/2 . 2 . 1^2 = 1 (m)
s2 = v02 . t ( t = t2 = 5s )
= 2 . 5 = 10 (m)
a03 = ( v3 - v03 ) / t3
= ( 0 - 2 ) / 2
= -1 (m/s)
=> s3 = v03 . t + 1/2 .a3 .t^2 (t=t3=2s)
= 2 . 2 + 1/2 . (-1) . 2^2
= 2 (m)
==> S = s1 + s2 + s3
= 1 + 10 + 2
= 13 (m)
Đúng 2
Bình luận (0)
Tham thảo :
a) v1 = v01 + a1 . t = 2t
t1 = 1 (s) => v2 = v1 = 2 . 1 = 2(m/s)
b) s1 = v01 . t + 1/2 . a1 . t^2 = 0 . 1 + 1/2 . 2 . 1^2 = 1 (m)
s2 = v02 . t ( t = t2 = 5s )
= 2 . 5 = 10 (m)
a03 = ( v3 - v03 ) / t3
= ( 0 - 2 ) / 2
= -1 (m/s)
=> s3 = v03 . t + 1/2 .a3 .t^2 (t=t3=2s)
= 2 . 2 + 1/2 . (-1) . 2^2
= 2 (m)
==> S = s1 + s2 + s3
= 1 + 10 + 2
= 13 (m)
Đúng 0
Bình luận (0)
1) Một thang máy chuyển động xuống dưới từ vận tốc đầu bằng 0, được chia làm 3 giai đoạn:
- Giai đoạn 1: Chuyển động nhanh dần đều trong thời gian 4s thì đạt vận tốc 4 m/s
- Giai đoạn 2: Chuyển động thẳng đều trong thời gian 5s
-Giai đoạn 3: Chuyển động chậm dần đều trong thời gian 8s thì dừng lại. Tính quãng đường thang máy đi được.
Tóm tắt:
\(v_0=0\) m/s
v=4 m/s
\(t_0=0\) s
\(t_1=4\) s
\(t_2=5\) s
\(t_3=8\) s
\(s=?\)km
Giải
Gia tốc của thang máy trong giai đoạn 1 là
\(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{t_1-t_0}=\dfrac{4-0}{4-0}=1\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 1 là
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=0\cdot4+\dfrac{1}{2}\cdot1\cdot4^2=8\left(m\right)\)
Quãng đường thang máy chuyển động trong giai đoạn 2 là
\(s_2=v\cdot t_2=4\cdot5=20\left(m\right)\)
Gia tốc của thang máy trong giai đoạn 2 là
\(a'=\dfrac{\Delta v'}{\Delta t'}=\dfrac{v-v_0}{t_3}=\dfrac{4-0}{8}=\dfrac{1}{2}\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 3 là
\(s_3=v_0t_3+\dfrac{1}{2}a't_3^2=0\cdot8+\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot8^2=16\left(m\right)\)
Quãng đường di chuyển dc của thang máy là
\(s_1+s_2+s_3=8+20+16=44\left(m\right)\)
Đúng 1
Bình luận (0)




















