Mm ơi giúp mình câu 52 đến 54 với nhớ làm dấu đẳng thức xảy ra luôn mình cảm ơn
Những câu hỏi liên quan
Giúp mình bài 55 đến 59 với và làm luôn dấu đẳng thức xảy ra
55.
\(3c^2\ge b^2+b^2+a^2\ge\dfrac{1}{3}\left(b+b+a\right)^2=\dfrac{1}{3}\left(2b+a\right)^2\)
\(\Rightarrow9c^2\ge\left(2b+a\right)^2\Rightarrow3c\ge2b+a\)
Do đó:
\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\ge\dfrac{9}{3c}=\dfrac{3}{c}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
Đúng 0
Bình luận (0)
56.
\(\dfrac{x^2\left(y+z\right)}{yz}\ge\dfrac{4x^2\left(y+z\right)}{\left(y+z\right)^2}=\dfrac{4x^2}{y+z}\)
Tương tự:
\(\dfrac{y^2\left(z+x\right)}{zx}\ge\dfrac{4y^2}{z+x}\) ; \(\dfrac{z^2\left(x+y\right)}{xy}\ge\dfrac{4z^2}{x+y}\)
Cộng vế với vế:
\(P\ge\dfrac{4x^2}{y+z}+\dfrac{4y^2}{z+x}+\dfrac{4z^2}{x+y}\ge\dfrac{4\left(x+y+z\right)^2}{2\left(x+y+z\right)}=2\left(x+y+z\right)=2\)
Vậy \(P_{min}=2\) khi \(x=y=z=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
57.
\(\dfrac{a^2}{b+c-a}+\dfrac{b^2}{c+a-b}+\dfrac{c^2}{a+b-c}\ge\dfrac{\left(a+b+c\right)^2}{b+c-a+c+a-b+a+b-c}=\dfrac{\left(a+b+c\right)^2}{a+b+c}=a+b+c\)
Dấu "=" xảy ra khi \(a=b=c\)
58.
\(VT=\dfrac{a\left(1+c\right)+b\left(1+a\right)+c\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}=\dfrac{ab+bc+ca+a+b+c}{1+a+b+c+ab+bc+ca+abc}\)
\(VT\ge\dfrac{ab+bc+ca+a+b+c}{a+b+c+ab+bc+ca+2}\)
Nên ta chỉ cần chứng minh:
\(\dfrac{ab+bc+ca+a+b+c}{a+b+c+ab+bc+ca+2}\ge\dfrac{3}{4}\)
\(\Leftrightarrow a+b+c+ab+bc+ca\ge6\)
Điều này hiển nhiên đúng do: \(a+b+c+ab+bc+ca\ge6\sqrt[6]{\left(abc\right)^3}=6\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Giúp mình 3 bài này với với lại làm luôn dấu bằng xảy ra mình cảm ơn
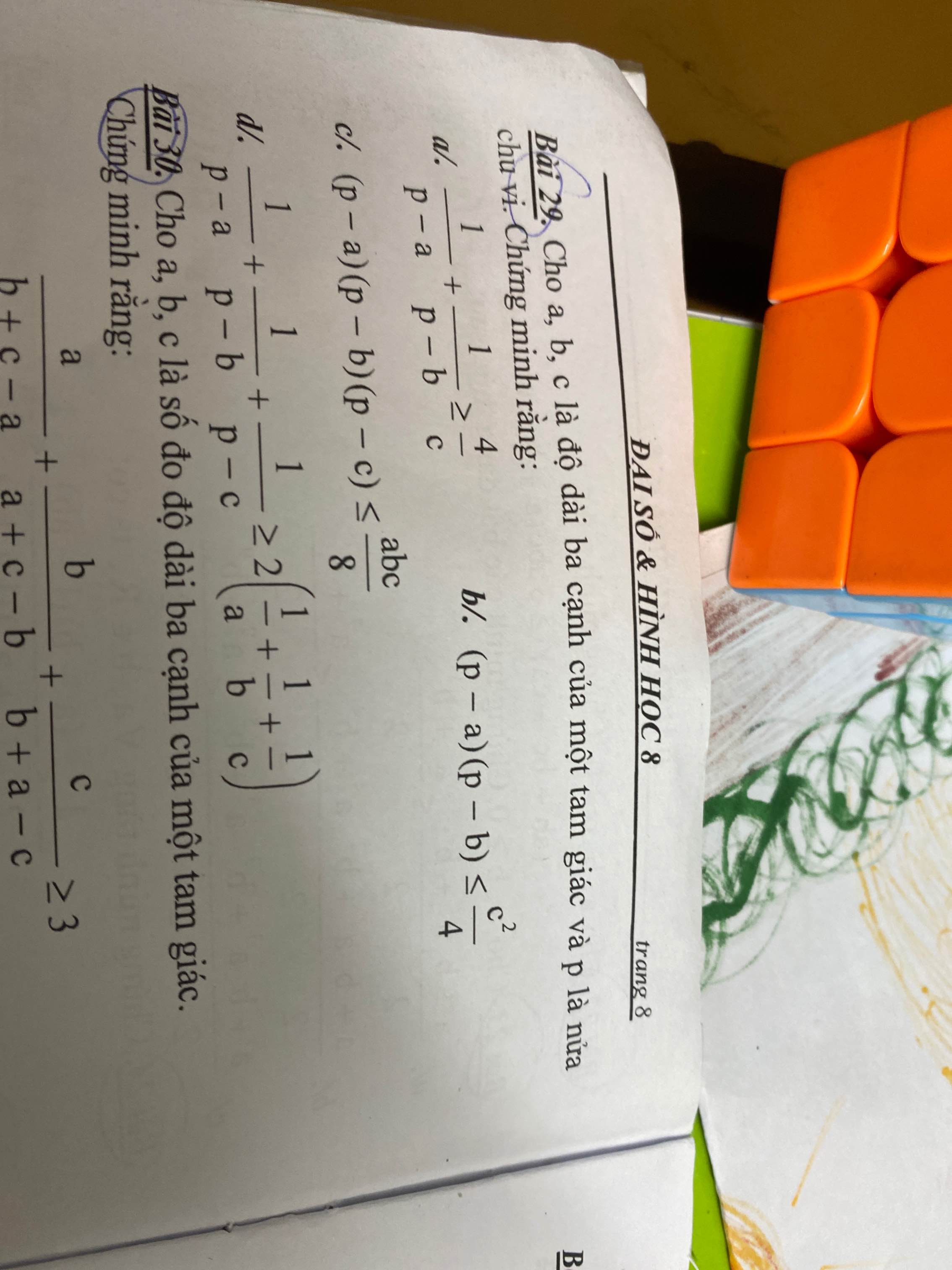
Giải giúp mình câu 52 với (chi tiết lời giải luôn) mình cảm ơn ạ
nKMnO4 = 14,2/158 ≃ 0,0899 mol
2KMnO4 + 16HCl → 2KCl + 2MnCl2 + 5Cl2 + 8H2O
0,0899 \(\dfrac{0,0899\times5}{2}\)
→ nCl2 = 0,22475 mol → VCl2 = 22,4.nCl2 = 5,0344 lít
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình câu 4 5 6 7 với, mình cảm ơn rất nhiều luôn❤️
1. While I was staying in Paris last summer, I met her.
2. When we were having dinner, there was a knock at the door.
3. When did you start studying English.
4. He used to visit me on Sundays when he studied in England.
5. Saving some pocket money for charity work is meaningful.
6. Our children find it interesting to give away their old books to needy people.
7. It's a year since we last saw Mary.
Đúng 3
Bình luận (1)
Những đẳng thức đáng nhớ
( 4x + 1)^2
( a + 2) ^2
Mình làm bằng hai cách cô dạy nhưng có cách thì ra mũ này, mũ kia. Giúp mình với T.T chỉ mình cách làm luôn nhé
1 Bảy hàng đẳng thức đáng nhớ:
1. (A +B)2 = A2 + 2AB + B2
2. (A - B)2 = A2 - 2AB +B2
3. A2 - B2 = (A - B).(A + B)
4. (A + B)3 = A3 +3A2B +3AB2 +B3
5. (A - B)3 = A3 - 3A2B - 3AB2 -B3
6. A3 + B3 = (A+B).(A2 - AB +B2)
7. A3 - B3 = (A-B) . (A2 + AB + B2)
Chú ý: Các hàng đẳng thức (4) và (5) nhiều khi còn được viết dưới dạng sau:
(A + B)3 = A3 + B3 +3AB.( A + B)
(A - B)3 = A3 - B3 - 3AB.(A - B)
2 Bình phương một tổng N hạng tử:
3 Mở rộng( nhị thức newton)
Định lí này nằm trong đặc biệt đã được giảng dạy ở các trung học và mang tên là các Hằng đẳng thức đáng nhớ
Ví dụ: điển hình nhất là nhị thức là công thức bình phương của x + y
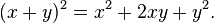
Hệ số nhị thức xuất hiện ở phép triển khai này tương ứng với hàng thứ ba của tam giác Pascal. Các hệ số có lũy thừa cao hơn của x + y tương ứng với các hàng sau của tam giác:
![\begin{align} (x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\[8pt] (x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, \\[8pt] (x+y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5, \\[8pt] (x+y)^6 & = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6, \\[8pt] (x+y)^7 & = x^7 + 7x^6y + 21x^5y^2 + 35x^4y^3 + 35x^3y^4 + 21x^2y^5 + 7xy^6 + y^7. \end{align}](https://upload.wikimedia.org/math/0/5/9/05912cb66ba1a0cc47688071d5cdae8a.png)
Tam giác Pascal
Chú ý rằng:
lũy thừa của x giảm dần cho tới khi đạt đến 0 (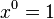
), giá trị bắt đầu là n (n trong 
.)lũy thừa của y tăng lên bắt đầu từ 0 (
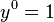) cho tới khi đạt đến n (n trong .)hàng nth của tam giác Pascal sẽ là các hệ số của nhị thức mở rộng (chú ý rằng đỉnh là hàng 0)với mỗi hàng, tích số (tổng của các hệ số) bằng 
.với mỗi hàng, nhóm tích số bằng 
.Định lý nhị thức có thể áp dụng với lũy thừa của bất cứ nhị thức nào. Ví dụ:
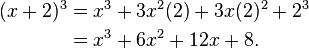
Với một nhị thức có phép trừ, định lý có thể được áp dụng khi sử dụng phép nghịch đảo số hạng thứ hai.
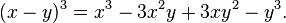
4.Bài tập:
16. Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu;
a) x2 + 2x + 1; b) 9x2 + y2 + 6xy;
c) 25a2 + 4b2 – 20ab; d) x2 – x + .
Bài giải:
a) x2 + 2x + 1 = x2+ 2 . x . 1 + 12
= (x + 1)2
b) 9x2 + y2+ 6xy = (3x)2 + 2 . 3 . x . y + y2 = (3x + y)2
c) 25a2 + 4b2– 20ab = (5a)2 – 2 . 5a . 2b + (2b)2 = (5a – 2b)2
Hoặc 25a2 + 4b2 – 20ab = (2b)2 – 2 . 2b . 5a + (5a)2 = (2b – 5a)2
d) x2 – x + = x2 – 2 . x .
+
=
Hoặc x2 – x + =
- x + x2 =
- 2 .
. x + x2 =
17. Chứng minh rằng:
(10a + 5)2 = 100a . (a + 1) + 25.
Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.
Áp dụng để tính: 252, 352, 652, 752.
Bài giải:
Ta có: (10a + 5)2 = (10a)2 + 2 .10a . 5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25.
Cách tính nhaame bình thường của một số tận cùng bằng chữ số 5;
Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được
(10a + 5)2 = 100a(a + 1) + 25
Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.
Áp dụng;
- Để tính 252 ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.
- Để tính 352 ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.
- 652 = 4225
- 752 = 5625.
18. Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:
a) x2 + 6xy + … = (… + 3y)2;
b) ... – 10xy + 25y2 = (… - …)2;
Hãy nêu một số đề bài tương tự.
Bài giải:
a) x2 + 2 . x . 3y + … = (…+3y)2
x2 + 2 . x . 3y + (3y)2 = (x + 3y)2
Vậy: x2 + 6xy +9y2 = (x + 3y)2
b) …-2 . x . 5y + (5y)2 = (… - …)2;
x2 – 2 . x . 5y + (5y)2 = (x – 5y)2
Vậy: x2 – 10xy + 25y2 = (x – 5y)2
Đề bài tương tự: Chẳng hạn:
4x + 4xy + … = (… + y2)
… - 8xy + y2 = (… - …)2
20. Nhận xét sự đúng, sai của kết quả sau:
x2 + 2xy + 4y2 = (x + 2y)2
Bài giải:
Nhận xét sự đúng, sai:
Ta có: (x + 2y)2 = x2 + 2 . x . 2y + 4y2
= x2 + 4xy + 4y2
Nên kết quả x2 + 2xy + 4y2 = (x + 2y)2 sai.
21. Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) 9x2 – 6x + 1; b) (2x + 3y)2 + 2 . (2x + 3y) + 1.
Hãy nêu một đề bài tương tự.
Bài giải:
a) 9x2 – 6x + 1 = (3x)2 – 2 . 3x . 1 + 12 = (3x – 1)2
Hoặc 9x2 – 6x + 1 = 1 – 6x + 9x2 = (1 – 3x)2
b) (2x + 3y) = (2x + 3y)2 + 2 . (2x + 3y) . 1 + 12
= [(2x + 3y) + 1]2
= (2x + 3y + 1)2
Đề bài tương tự. Chẳng hạn:
1 + 2(x + 2y) + (x + 2y)2
4x2 – 12x + 9…
22. Tính nhanh:
a) 1012; b) 1992; c) 47.53.
Bài giải:
a) 1012 = (100 + 1)2 = 1002 + 2 . 100 + 1 = 10201
b) 1992= (200 – 1)2 = 2002 – 2 . 200 + 1 = 39601
c) 47.53 = (50 – 3)(50 + 3) = 502 – 32 = 2500 – 9 = 2491.
23. Chứng minh rằng:
(a + b)2 = (a – b)2 + 4ab;
(a – b)2 = (a + b)2 – 4ab.
Áp dụng:
a) Tính (a – b)2 , biết a + b = 7 và a . b = 12.
b) Tính (a + b)2 , biết a - b = 20 và a . b = 3.
Bài giải:
a) (a + b)2 = (a – b)2 + 4ab
- Biến đổi vế trái:
(a + b)2 = a2 +2ab + b2 = a2 – 2ab + b2 + 4ab
= (a – b)2 + 4ab
Vậy (a + b)2 = (a – b)2 + 4ab
- Hoặc biến đổi vế phải:
(a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + 2ab + b2
= (a + b)2
Vậy (a + b)2 = (a – b)2 + 4ab
b) (a – b)2 = (a + b)2 – 4ab
Biến đổi vế phải:
(a + b)2 – 4ab = a2 +2ab + b2 – 4ab
= a2 – 2ab + b2 = (a – b)2
Vậy (a – b)2 = (a + b)2 – 4ab
Áp dụng: Tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4 . 12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4 . 3 = 400 + 12 = 412
24. Tính giá trị của biểu thức 49x2 – 70x + 25 trong mỗi trường hợp sau:
a) x = 5; b) x = .
Bài giải:
49x2 – 70x + 25 = (7x)2 – 2 . 7x . 5 + 52 = (7x – 5)2
a) Với x = 5: (7 . 5 – 5)2 = (35 – 5)2 = 302 = 900
b) Với x = : (7 .
– 5)2 = (1 – 5)2 = (-4)2 = 16
Bài 25. Tính:
a) (a + b + c)2; b) (a + b – c)2;
c) (a – b – c)2
Bài giải:
a) (a + b + c)2 = [(a + b) + c]2 = (a + b)2 + 2(a + b)c + c2
= a2+ 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2bc + 2ac.
b) (a + b – c)2 = [(a + b) – c]2 = (a + b)2 - 2(a + b)c + c2
= a2 + 2ab + b2 - 2ac - 2bc + c2
= a2 + b2 + c2 + 2ab - 2bc - 2ac.
c) (a – b –c)2 = [(a – b) – c]2 = (a – b)2 – 2(a – b)c + c2
= a2 – 2ab + b2 – 2ac + 2bc + c2
= a2 + b2 + c2 – 2ab + 2bc – 2ac.
Bài 26. Tính:
a) (2x2 + 3y)3; b) (x – 3)3
Bài giải:
a) (2x2 + 3y)3 = (2x2)3 + 3(2x2)2 . 3y + 3 . 2x2 . (3y)2 + (3y)3
= 8x6 + 3 . 4x4 . 3y + 3 . 2x2 . 9y2 + 27y3
= 8x6 + 36x4y + 54x2y2 + 27y3
b) (x – 3)3 =
- 3
. 3 + 3
. 32 - 33
= x3 – 3 .
x2 . 3 + 3 .
x . 9 – 27
= x3 –
x2 +
x - 27
Bài 27. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a) – x3 + 3x2 – 3x + 1;
b) 8 – 12x + 6x2 – x3.
Bài giải:
a) – x3 + 3x2– 3x + 1 = 1 – 3 . 12 . x + 3 . 1 . x2 – x3
= (1 – x)3
b) 8 – 12x + 6x2 – x3 = 23 – 3 . 22. x + 3 . 2 . x2 – x3
= (2 – x)3
Bài 28. Tính giá trị của biểu thức:
a) x3 + 12x2 + 48x + 64 tại x = 6;
b) x3 – 6x2 + 12x- 8 tại x = 22.
Bài giải:
a) x3 + 12x2 + 48x + 64 = x3 + 3 . x2. 4 + 3 . x . 42 + 43
= (x + 4)3
Với x = 6: (6 + 4)3 = 103 = 1000
b) x3 – 6x2 + 12x- 8 = x3 – 3 . x2. 2 + 3 . x . 22 - 23
= (x – 2)3
Với x = 22: (22 – 2)3 = 203 = 8000
Bài 29. Đố: Đức tính đáng quý.
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tổng hoặc một hiệu, rồi điền chữ cùng dòng với biều thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.
x3 – 3x2 + 3x – 1 N
16 + 8x + x2 U
3x2 + 3x + 1 + x3 H
1 – 2y + y2 Â
Bài giải:
Ta có:
N: x3 – 3x2 + 3x – 1 = x3 – 3 . x2. 1+ 3 . x .12 – 13 = (x – 1)3
U: 16 + 8x + x2= 42 + 2 . 4 . x + x2 = (4 + x)2
= (x + 4)2
H: 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1
= (x + 1)3 = (1 + x)3
Â: 1 – 2y + y2 = 12 - 2 . 1 . y + y2 = (1 - y)2
= (y - 1)2
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Chú ý:
Có thế khai triển các biểu thức (x – 1)3 , (x + 1)3 , (y - 1)2 , (x + 4)2 ... để tìm xem kết quả ứng với chữ nào và điền vào bảng.
Đúng 0
Bình luận (0)
Ta có:
Áp dụng hằng đăng thức bình phương của một tổng.
\(\left(A+B\right)^2=A^2+2AB+B^2\)
Thay vào sẽ là:
\(\left(4x+1\right)^2=16x^2+8x+1\)
\(\left(a+2\right)^2=a^2+4a+4\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Các bạn giúp mình với mình cảm ơn các bạn.
Các bạn ơi mình sắp làm bài thi rồi mình gấp rút lắm luôn nha các bạn.
Tìm xinZ để biểu thức Max:a) A frac{1}{7x}b) Bfrac{14-x}{4-x}c) C frac{27-2x}{12-x}MẤY BẠN TỐT BỤNG ƠI LÀM ƠN GIÚP MÌNH VỚI!! MAI MÌNH CẦN LUÔN RỒI! LÀM ƠN HÃY GIÚP MÌNH, MÌNH XIN HẬU TẠ BẰNG VIỆC TICK CHO CÁC BẠN ( À, AI TỐT GIÚP MÌNH GIẢI BÀI THÌ NHỚ GHI RÕ CÁCH LÀM HỘ MÌNH NHÉ!!!) MÌNH CẢM ƠN NHIỀU NHIỀU LẮM LẮM!!
Đọc tiếp
Tìm x\(\in\)Z để biểu thức Max:
a) A= \(\frac{1}{7x}\)
b) B=\(\frac{14-x}{4-x}\)
c) C= \(\frac{27-2x}{12-x}\)
MẤY BẠN TỐT BỤNG ƠI LÀM ƠN GIÚP MÌNH VỚI!! MAI MÌNH CẦN LUÔN RỒI! LÀM ƠN HÃY GIÚP MÌNH, MÌNH XIN HẬU TẠ BẰNG VIỆC TICK CHO CÁC BẠN ( À, AI TỐT GIÚP MÌNH GIẢI BÀI THÌ NHỚ GHI RÕ CÁCH LÀM HỘ MÌNH NHÉ!!!) MÌNH CẢM ƠN NHIỀU NHIỀU LẮM LẮM!!
a, A lớn nhất khi 7x la nguyên dương nho nhất
\(\Rightarrow7x=1\)
\(\Rightarrow x=\frac{1}{7}\)
\(b,B=\frac{10+4-x}{4-x}\)
\(B=\frac{10}{4-x}+1\)
b lon nhat khi 4-xla nguyen duong nho nhat
\(\Rightarrow4-x=1\)
\(\Rightarrow x=4-1=3\)
\(c,C=\frac{27-2x}{12-x}=\frac{3+24-2x}{12-x}=\frac{3}{12-x}+2\)
c lon nhat khi 12-x la nguyen duong nho nhat
\(\Rightarrow12-x=1\Rightarrow x=11\)
Đúng 0
Bình luận (0)
Các bạn ơi soạn sinh như thế nào vậy chỉ cho mình nhé bạn nào đã học sinh lớp 6 mà nhớ thì chỉ giúp mình nhà còn nếu có sách mà làm đến với lại bít thì bày cho mình nha mình cảm ơn.
Dễ lắm chỉ cần gõ bài 1 sinh .... trang ....
Rồi vào bài giảng hoặc violet
Đúng 0
Bình luận (2)
trường mk ko cần soạn
mk chỉ cần lên lp hok bài xonng rồi làm bài tập thui
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu chuyện "Ếch ngồi Đáy giếng" làm em nhớ lại chuyện đã xảy ra vs em hoặc bạn em. Hãy kể lại câu chuyện đó?
Comment Giúp mình nha !!!
P/s: Cảm ơn mn nhìu! ahihi
mik phải tưởng tượng ra
Vd mik và nga đã xảy ra xích mích với nhau(nêu cuộc đối thoại cho hấp dẫn)
mik đổ tội cho nga là lấy bút của mik
.......(kể ra cho hấp dẫn)
Đúng 0
Bình luận (1)
-Trong h ... ,mình được cô giáo khen
- Ra chơi,huyênh hoang với ban bè
- Biết là tiết sau kiểm tra nhưng không học
- Cô giáo bước vào lớp, ra đề
-Đề khó (vì không ôn bài)
- Nhìn quanh lớp, các bạn đang miệt mài làm
- Lo lắng, trả lời lung tung vào bài kiểm tra
- 15' sau, cô giáo thu bài
- Cuối h, buồn khi biết mình bị điểm kém
- Rút ra bài học quý giá cho bản thân
Đúng 0
Bình luận (1)
Tối thứ bảy hàng tuần, tôi đều được bà kể cho nghe truyện ngày xưa. Trong đó có những câu chuyện ngụ ngôn tuy ngắn nhưng thật hay và bổ ích, giúp con người thấy được nhiều bài học trong cuộc sống. Hôm nay, bà đã kể cho tôi chuyện “Ếch ngồi đáy giếng”.
Bà nội tôi thuộc rất nhiều ca dao, tục ngữ, thành ngữ... Vì thế khi nói chuyện bả hay chêm vào đó những câu tục ngữ lạ mà tôi không hiểu. Những lúc như thế bà lại cặn kẽ giảng giải. Hôm nay, bà nói về câu tục ngữ “Ếch ngồi đáy giếng” chỉ những kẻ dù hiểu biết rất cạn hẹp nhưng lúc nào cũng huyênh hoang, tự đắc. Rồi để giải thích cho tôi hiểu hơn, bà kể lại cho tôi nguồn gốc câu thành ngữ ấy.
Ngày xưa, có một chú ếch sống trong một cái giếng nhỏ. Vì sống ở đó lâu ngày nên nó không biết thế giới ở ngoài kia ra sao. Xung quanh nó chỉ có vài con cua, ốc, nhái bé nhỏ... nên tưởng rằng mình là to là mạnh nhất. Ếch ta tự hào lắm về tiếng kêu ồm ộp của mình. Mỗi khi nó kêu làm vang động cá cái giếng nhỏ, khiến những con vật kia rất hoảng sợ. Ếch cứ ngỡ mình rất oai. Ngẩng mặt lên nhìn trời, nó thấy bầu trời chỉ bằng chiếc vung chứ không cao và rộng lớn như người ta thường đồn đại. Ểch ta kiêu hãnh lắm và cho rằng trời quá bé nhỏ còn nó mới xứng là một vị chúa tể. Suy nghĩ ấy đã làm cho ếch ta coi thường mọi vật. Trong cái nhìn của ếch thì chẳng có ai bằng nó cả. Thế nên, một năm trời mưa to, nước trong giếng dâng cao, đưa ếch ta ra ngoài. Quen cái nhìn cũ, quen cách nghĩ cũ, ếch huyênh hoang đi lại trên đường, đi khắp nơi như chốn không người. Theo thói quen, nó cất tiếng kêu ồm ộp và tưởng rằng ai cũng sợ như dưới đáy giếng kia. Nó đưa cặp mắt lên nhìn và vẫn cho rằng bầu trời bé tẹo như cái vung nên chẳng để ý gì đến xung quanh. Bỗng nó thấy tối sầm lại, không nhìn rõ gì nữa. Một vật gì rất lớn che mất tầm nhìn của nó. Nó đâu biết rằng đó là chân của một con trâu nên đã bị giẫm bẹp. Thế là hết đời một con ếch ngông nghênh.
Nghe câu chuyện bà kể, tôi thấy chú ếch con thật đáng chê trách. Những người trẻ, ít kinh nghiệm, hiểu biết nhưng lại là những người có tính cách hung hăng, huyênh hoang, ngông nghênh nhiều nhất. Có lẽ vì còn chưa hiểu biết nhiều nên họ mới làm những việc kém hiểu biết. Vì thế, những người trẻ tuổi phải cố gắng mở rộng tầm hiểu biết của mình, không chỉ trong sách vở mà còn nhiều lĩnh vực khác, không chủ quan hay kiêu ngạo. Những tính cách đó chỉ làm hỏng một con người mà thôi, đôi khi còn làm cho người khác bị tổn thương nữa.
Bao giờ kể chuyện xong bà cũng giúp tôi rút ra những bài học quí báu, không cao sang, xa vời mà rất thực tế, gần gũi. Tôi luôn lắng nghe những điều bà dặn để áp dụng vào cuộc sống. Bản thân tôi cũng như tất cả mọi người, không ai là hoàn hảo nên luôn phải học hỏi lẫn nhau, những khiếm khuyết của mình sẽ được tri thức của người khác bổ sung và ngược lại. Do đó, không được giấu điểm yếu kém. Bà còn bảo tôi phải học thật chăm để không bị kém hiểu biết, có như thế mới không suy nghĩ hay hành động thiếu hiểu biết. Quả thực những điều bà dặn dò tôi đòi hỏi một sự cố găng nỗ lực và tự giác rất lớn nhưng dù thế nào tôi cũng không thể để mình như chú ếch ngồi đáy giếng được.
Truyện ngụ ngôn Ếch ngồi đáy giếng của ông cha ta thật sâu sắc: Nói chuyện của loài vật nhưng mục đích là nói chuỵện loài người. Bất kì ai khi đọc truyện cũng sẽ tự rút ra được cho mình bài học cần thiết và bổ ích.
# tham khảo nha#
Đúng 0
Bình luận (1)
Xem thêm câu trả lời