Giá trị x và y thoả mãn x^2 -2x+y^2 +4y+5=0 là (x;y)

Những câu hỏi liên quan
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
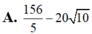
![]()
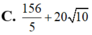
![]()
1) Tập hợp các số nguyên x để dfrac{x+3}{x+1} đạt giá trị nguyên là
2) Tính giá trị biểu thức Bdfrac{1+2+2^2+2^3+...+2^{2015}}{1-2^{2016}} ta được B
3) Tìm số có ba chữ số overline{abc} biết overline{1abc} chia cho overline{abc} dư 3.
4) Số nguyên y thoả mãn dfrac{y+5}{7-y}dfrac{2}{-5} là
5) Tập hợp các số tự nhiên n để Adfrac{11}{2n-3} nhận giá trị nguyên là
6) Số các số nguyên x thoả mãn 15-|-2x+3|.|5+4x|-19 là
Đọc tiếp
1) Tập hợp các số nguyên x để \(\dfrac{x+3}{x+1}\) đạt giá trị nguyên là
2) Tính giá trị biểu thức B=\(\dfrac{1+2+2^2+2^3+...+2^{2015}}{1-2^{2016}}\) ta được B=
3) Tìm số có ba chữ số \(\overline{abc}\) biết \(\overline{1abc}\) chia cho \(\overline{abc}\) dư 3.
4) Số nguyên y thoả mãn \(\dfrac{y+5}{7-y}=\dfrac{2}{-5}\) là
5) Tập hợp các số tự nhiên n để A=\(\dfrac{11}{2n-3}\) nhận giá trị nguyên là
6) Số các số nguyên x thoả mãn 15-|-2x+3|.|5+4x|=-19 là
3, Gọi d là thương.
Theo đề ra ta có:
\(\dfrac{1\overline{abc}}{\overline{abc}}=d\) (dư 3)
\(\Rightarrow1000+\overline{abc}=\overline{abc}.d+3\)
\(\Rightarrow1000=\overline{abc}.\left(d-1\right)+3\)
\(\Rightarrow\overline{abc}.\left(d-1\right)=997\)
Vì 997 là số nguyên tố và \(\overline{abc}\) có 3 chữ số \(\Rightarrow\overline{abc}=997\)
Đúng 0
Bình luận (0)
1) x +3 / x+1
Để x + 3/ x +1 nguyên thì :
x + 3 phải chia hết cho x + 1
=> x + 1 + 2 chia hết cho x + 1
=> x +1 chia hết cho x + 1
2 chia hết cho x +1
=> x + 1 thuộc Ư(2)
Lập bảng :
| x + 1 | -1 | 1 | 2 | -2 |
| x | -2 | 0 | 1 | -3 |
Vậy x = { -2;-3;0;1}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1:Cho a,b là các số nguyên tố thỏa mãn: (a-1) chia hết cho b và (b3 - 1) chia hết cho a.Chứng minh: a= b2+b+1
Bài 2:Cho x,y là hai số thực thỏa mãn:
x3 + y3 +3x2 + 4x + 3y2 +4y +4=0.Tìm giá trị lớn nhất của biểu thức P=1/x+1/y
1) Vì a, b là số nguyên tố và a - 1 chia hết cho b nên a là số nguyên tố lẻ >=3 và b =2( vì a -1 chẵn)
b3 - 1 = 7 chia hết cho a, nên a =7. Vậy a = b2 + b + 1( 7 = 22 + 2 + 1)
Đúng 0
Bình luận (0)
tập hợp các giá trị của x thoả mãn {x-1}X{x+2}=0
=> x - 1 = 0 => x = 1
hoặc x + 2 = 0 => x = -2
Vậy: x thuộc {-2;1}
Đúng 0
Bình luận (0)
Giả sử: x,y,z là các số thực dương thoả mãn \(x+z\le2y\) và \(x^2+y^2+z^2=1\)
Tìm giá trị lớn nhất của biểu thức \(P=\frac{xy}{1+z^2}+\frac{yz}{1+x^2}-y^3\left(\frac{1}{x^3}+\frac{1}{z^3}\right)\)
Bài 1:cho ba số x,y,z khác 0 thỏa mãn điều kiện:
y+z-x/x=z+x-y/y=x+y-z/z. Khi đó B= (1+x/y).(1+y+z).(1+z+x) có giá trị bằng.....
Bài 2:Giá trị nhỏ nhất của biểu thức A=(x^2-2x-q).(x^2-2x+3) là.....
GIẢI CHI TIẾT HỘ MÌNH NHÉ
ban sat long nhan natsu oi giai nhu vay thi ai hieu ham
Đúng 0
Bình luận (0)
bài 1
Từ tính chất dãy tỉ số bằng nhau ta có :
\(\frac{y+z-x}{x}=\frac{z+x-y}{y}=\frac{x+y-z}{z}=\frac{y+z-x+z+x-y+x+y-z}{x+y+x}=\frac{x+y+z}{x+y+z}=1\)
=> x=y=z
=> B = 2.2.2 = 8
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho x,y là số nguyên dương thoả mãn: x^2 +xy = 2y^2. Tính giá trị biểu thức A= (2013xy + 2x^2)/(2014x^ + 2xy)
\(x^2+xy-2y^2=0< =>\left(x-y\right)\left(x+2y\right)=0< =>\)x=y (vì x+2y>0 với x;y>0)
A= (2013x2+2x2)(2014x2+2x2) = 2015.2016.x4
Đúng 0
Bình luận (0)
Cho: \(x;y;z\) là các số thực thoả mãn điều kiện: \(\frac{3}{2}x^2+y^2+z^2+yz=1\)
Tìm giá trị lớn nhất của: \(A=x+y+z\)
\(\frac{3}{2}x^2+y^2+z^2+yz=1\Leftrightarrow3x^2+2y^2+2z^2+2yz=2\)
\(\Leftrightarrow\left(x^2+y^2+z^2+2xy+2yz+2zx\right)+\left(x^2-2xy+y^2\right)+\left(x^2-2xz+z^2\right)=2\)
\(\Leftrightarrow\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=2\)
Suy ra : \(A^2\le2\Rightarrow A\le\sqrt{2}\)
Vậy Max A = \(\sqrt{2}\) khi \(\hept{\begin{cases}x=y\\x=z\\x+y+z=\sqrt{2}\end{cases}\Leftrightarrow}x=y=z=\frac{\sqrt{2}}{3}\)
Đúng 0
Bình luận (0)
Cho các số dương x, y thoả mãn \(x\sqrt{x}+y\sqrt{y}=x^2+y^2=x^2\sqrt{x}+y^2\sqrt{y}.\)Tính giá trị của x + y .
Lời giải:
Điều kiện đề bài:
\(\Rightarrow \left\{\begin{matrix} x^2+y^2-x\sqrt{x}-y\sqrt{y}=0\\ x^2\sqrt{x}+y^2\sqrt{y}-x^2-y^2=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\sqrt{x}(\sqrt{x}-1)+y\sqrt{y}(\sqrt{y}-1)=0\\ x^2(\sqrt{x}-1)+y^2(\sqrt{y}-1)=0\end{matrix}\right.\)
\(\Rightarrow (x^2-x\sqrt{x})(\sqrt{x}-1)+(y^2-y\sqrt{y})(\sqrt{y}-1)=0\) (lấy vế 2 trừ vế 1)
\(\Leftrightarrow x\sqrt{x}(\sqrt{x}-1)^2+y\sqrt{y}(\sqrt{y}-1)^2=0\)
Vì mỗi số hạng trên đều không âm với mọi $x,y>0$ nên để tổng của chúng bằng $0$ thì:
\(x\sqrt{x}(\sqrt{x}-1)^2=y\sqrt{y}(\sqrt{y}-1)^2=0\)
\(\Rightarrow x=y=1\Rightarrow x+y=2\)
Đúng 0
Bình luận (0)