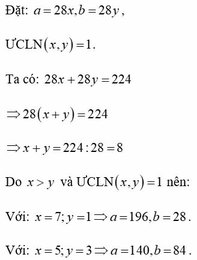a ) 140

b) 84

a=140.

b=84.

a=140

b=84

Tham khảo

a =28q ; b =28 p  ;(q;p)=1 ; q;p thuộc N và  q>p

a+b =224

=>28q+28p = 224 => q+p = 8

+q=7 => a =7.28 =196 ; p =1 => b =1.28 =28

+q=5 => a =5.28 =140; p =3 => 3.28 =84

Vậy a =196; b=28

hoặc a =140 ; b=84

Đặt a = 28a’, b = 28b’, ƯCLN (a’, b’) = 1.

Ta có 28a’ + 28b’ = 224

 28(a’ + b’) = 224

 a’ + b’ = 224 : 28 = 8.

Do a’ > b’ và ƯCLN (a’, b’) = 1 nên

a = 196 = 140
b = 28 = 84

Tham khảo

a =28q ; b =28 p  ;(q;p)=1 ; q;p thuộc N và  q>p

a+b =224

=>28q+28p = 224 => q+p = 8

+q=7 => a =7.28 =196 ; p =1 => b =1.28 =28

+q=5 => a =5.28 =140; p =3 => 3.28 =84

Vậy a =196; b=28

hoặc a =140 ; b=84

vì UCLN 2 số là 28 nên đặt a=28k, b=28p, k,p là số tự nhiên
ta có 28(k+p)=224=>k+q=8
vậy các cặp (a, b) thỏa mãn là (28,196), (56, 168), (84,140), (112, 112) 
và các hoán vị của nó.
câu 5
a) cột gần nhất là cột cách cột số 1 đoạn a. và a chính là bội chung nhỏ nhất của 20 và 15 => a=60
vậy cột số 60/20=3 ko phải trồng lại.
b) các cột ko phải trồng lại ở vị trí x. trong đó x là k/c tới cột thứ nhất và x chia hết cho 20 và 15
vậy x có thể là 60, 120, 180,240,300
ứng với các cột là 3,6,9,12,15

               nhe ban k minh nha minh gioi lam day

minh nhanh nhat

Ta có:UCLN(a,b)=28

\(\Rightarrow\)a=28m,b=28n vậy UCLN(m,n)=1

mà a>b \(\Rightarrow\)m>n

Ta còn có:a+b=224

      \(\Rightarrow\) 28m+28n=224

               28(m+n)=224

               m+n =224:28

               m+n=8

Mà m và n là hai số nguên tố cùng nhau và m>n

Nên:*m=7;n=1\(\Rightarrow\)a=28.7=196;b=28.1=28

       *m=5;n=3\(\Rightarrow\)a=28.5=140;b=28.3=84

Vậy a=196;b=28

hay:a=140;b=84

Đặt: a = 28x, b = 28y, ƯCLN(x,y) = 1.

Ta có: 28x + 28y = 224

=> 28(x+y) = 224

=> x+y = 224:28 = 8

Do x > y và ƯCLN(x,y) = 1 nên:

Với: x = 7; y = 1=> a = 196; b = 28.

Với: x = 5; y = 3 => a = 140, b = 84

a=28p ; b = 28q     (p;q) =1 p>q

a+b =28p+28q =224

=> p+q=8

             => p=7 ; q=1 => a =28.7=196  ;   b = 28; 

             => p=5 ; q =3 =>  a= 28.5 =140 ;  b= 28.3 =84