Giải phương trình nghiệm nguyên:
a) \(x!+y!=\left(x+y\right)!\)
b) \(x^{17}+y^{17}=19^{17}\)
Bài 1 : Tìm các số tự nhiên \(x\) thoả mãn : \(2^x+3^x=35\)
Bài 2 : Tìm \(x;y\inℤ^+\) thoả mãn : \(x!+y!=\left(x+y\right)!\)
Bài 3 : Chứng minh rằng phương trình sau không có nghiệm nguyên :
\(x^{17}+y^{17}=19^{17}\)
Bài 1: Bài này số nhỏ nên chỉ cần chặn miền giá trị của \(x\) rồi xét các trường hợp thôi nhé. Ta thấy \(3^x< 35\Leftrightarrow x\le3\). Nếu \(x=0\) thì \(VT=2\), vô lí. Nếu \(x=1\) thì \(VT=5\), cũng vô lí. Nếu \(x=2\) thì \(VT=13\), vẫn vô lí. Nếu \(x=3\) thì \(VT=35\), thỏa mãn. Vậy, \(x=3\).
Bài 2: Nếu \(x=0\) thì pt đã cho trở thành \(0!+y!=y!\Leftrightarrow0=1\), vô lí,
Nếu \(x=y\) thì pt trở thành \(2x!=\left(2x\right)!\) \(\Rightarrow\left(x+1\right)\left(x+2\right)...\left(2x\right)=2\) \(\Leftrightarrow x=1\Rightarrow y=1\)
Nếu \(x\ne y\) thì không mất tính tổng quát, giả sử \(1< y< x\) thì \(x!+y!< 2x!\le\left(x+1\right)x!=\left(x+1\right)!< \left(x+y\right)!\) nên pt đã cho không có nghiệm trong trường hợp này.
Như vậy, \(x=y=1\)
Bài 3: Bổ sung đề là pt không có nghiệm nguyên dương nhé, chứ nếu nghiệm nguyên thì rõ ràng \(\left(x,y\right)=\left(0,19\right)\) là một nghiệm cũa pt đã cho rồi.
Giả sử pt đã cho có nghiệm nguyên dương \(\left(x,y\right)\)
Khi đó \(x,y< 19\). Không mất tính tổng quát ta có thể giả sử \(1< y\le x< 19\). Khi ấy \(x^{17}+y^{17}=19^{17}\ge\left(x+1\right)^{17}=x^{17}+17x^{16}+...>x^{17}+17x^{16}\), suy ra \(y^{17}>17x^{16}\ge17y^{16}\) \(\Rightarrow y>17\). Từ đó, ta thu được \(17< y\le x< 19\) nên \(x=y=18\). Thử lại thấy không thỏa mãn.
Vậy pt đã cho không có nghiệm nguyên dương.
Chị độc giải sau khi em biết làm thôi à.
Giải phương trình nghiệm nguyên:
\(x^{17}+y^{17}=19^{17}\)
Giải phương trình nghiệm nguyên
a) \(x^2+6x+17^{91}=2016^{2020}\)
b) \(x^2+2017^{2019}=2016\left(y-1\right)^2\)
c) \(x^2-2x=2017^{2017}\)
d) \(x^2+4x=2018^{10}\)
Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.
Giải phương trình nghiệm nguyên \(x^2+4y^2+28=17\left(x^4+y^4+14y^2+49\right)\)
mày bị ngáo ak. đã xấu còn bị điên. đã bị điên cò học dốt
y^2+7=z
\(\Leftrightarrow x^2+4z=17\left(x^4+z^2\right)\)Hiển nhiên \(VP\ge VT\) đẳng thức chỉ xẩy ra khi x=z=0
với z=0=> y^2+7=0 vô nghiệm
KL vô nghiệm nguyên
Giải hệ phương trình \(\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=8\\x\left(x+1\right)+y\left(y+1\right)+xy=17\end{cases}}\)
Hệ tương đương với: \(\hept{\begin{cases}xy+x+y=7\\x^2+y^2+x+y+xy=7\end{cases}}\)
Đặt \(x+y=a;xy=b\)ta có: \(x^2+y^2=a^2-2b\)
Thay vào hệ ta có:
\(\hept{\begin{cases}b+a=7\\a^2-b+a=17\end{cases}}\)
\(\Rightarrow a^2+2a+1=25\Rightarrow a+1^2=25\)
Đến đây tìm a,b sau đó ta tìm được:
(x,y)=(1,3);(3,1)
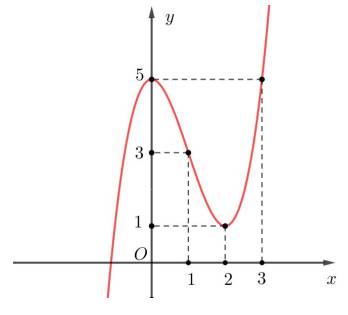
Cho hàm số y=f(x) có đồ thị như hình vẽ. Hỏi phương trình \(f\left(x^3-2x^2+14x+\sqrt{17}\right)=\sqrt{17}\) có bao nhiêu nghiệm thực?
Giải hệ phương trình :
\(\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=8\\x\left(x+1\right)+y\left(y+1\right)+xy=17\end{cases}}\)
Hệ đã cho tương ứng với :
\(\hept{\begin{cases}x+y+xy=7\\\left(x+y\right)^2-xy+x+y=17\end{cases}}\)
Đătl \(x+y=S;xy=P\) , giải hệ trên ta được : \(\hept{\begin{cases}S=4\\P=3\end{cases}}\)hoặc \(\hept{\begin{cases}S=-6\\P=13\end{cases}}\)
Thep định lí Vi-ét đảo thì x , y là các nghiệm của phương trình:
\(t^2-4t+3=0\) hoặc \(t^2+6t+13=0\)
Từ đó được 2 nghiệm của hệ là :
\(\left(x;y\right)\in\left\{\left(1;3\right);\left(3;1\right)\right\}\)
\(\left(x^2+4y^2+28\right)^2=17\left(x^4+y^4+14y^2+49\right)\)
Tìm các nghiệm tự nhiên (x,y) của phương trình
\(\left(x^2+4z\right)^2=17\left(x^4+z^2\right)\)
\(x^4+8x^2z+16z^2=17x^4+17z^2\)
\(t^4-2t^2z+z^2=\left(t^2-z\right)^2=0\)
Nghiệm duy nhất: \(t^2=z\Rightarrow t^2=y^2+7\Rightarrow\hept{\begin{cases}t=4\Rightarrow x=2\\y=3\end{cases}}\)KL (x,y)=(2,3)
bài 5 :tìm x, y thuộc Z biết: 1) -x=-7
2) -x=17. 3) |x| =17. 4) -(-x)=|-17| 5) -19-x=17. 6)-19-x=-17. 7) -5-(10-x)=7. 8)|x+3|+7= 12. 9) 2-|x-2| =x. 10)\(^{ }\left(X-2^{ }\right)^2\) = \(^{ }\left(x-2\right)^6\) 11) x.y + x+y =9. 12) 5.xy + x+y =3
( Mik làm mấy phần mà bạn dưới chưa làm)
11) xy+x+y=9
\(\Leftrightarrow\) xy+x+y+1=9+1
\(\Leftrightarrow\left(xy+x\right)+\left(y+1\right)\)=10
\(\Leftrightarrow x\left(y+1\right)+\left(y+1\right)=10\)
\(\Leftrightarrow\) (x+1)(y+1)=10=1.10=10.1=-1.-10=-10.-1=2.5=5.2=-2.-5=-5.-2
\(\Rightarrow\) TH1: x+1=1 ; y+1=10
\(\Leftrightarrow x=0;y=9\)
TH2: x+1=10;y+1=1
\(\Leftrightarrow\)x=9;y=0
TH3: x+1=-1;y+1=-10
\(\Leftrightarrow\) x=-2;y=-11
...........
Vậy:........
( Bạn tự làm nốt chứ dài quá, mik chỉ hướng dẫn cách làm bài thôi)
1) -x = -7
=> x = 7
2) - x = 17
=> x = - 17
3) |x| = 17
=> x = ±17
4) -(-x) = |-17|
=> x = 17
5) - 19 - x = 17
=> - x = 17 + 19
=> x = - 36
6) - 19 - x = - 17
=> - x = - 17 + 19
=> -x = 2
=> x = - 2
7) - 5 - (10 - x) = 7
=> - 5 - 10 + x = 7
=> - 15 + x = 7
=> x = 7 + 15
=> x = 22
8) |x + 3| + 7 = 12
=> |x + 3| = 12 - 7
=> |x + 3| = 5
=> x + 3 = 5 hoặc x + 3 =- 5
=> x = 2 hoặc x = - 8
9) 2 - |x - 2| = x
=> - |x - 2| - x = - 2
TH1: x >= 2
- (x - 2) - x = - 2
=> - x + 2 - x =- 2
=> - 2x = - 4
=> x = 2 (nhận)
TH2: x < 2
-[-(x - 2)] - x = - 2
=> x - 2 - x = - 2
=> 0x = 0 (vô số nghiệm)