Cho tứ giác ABCD, các tia phân giác của 4 góc cắt nhau tại M, N, P, Q. Chứng minh MNPQ là tứ giác có tổng các góc đối diện bù nhau
Những câu hỏi liên quan
cho tứ giác ABCD các đừng phân giác của góc A;B;C;D .Đường này cắt đường kia tại M;N;P;Q.Chứng minh rằng tứ giác MNPQ là tứ giác có tổng các góc đối diện bù nhau
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tứ giác ABCD các đường phân giác của các góc A, góc B, góc C, góc D đường này cắt đường kia tại M, N, P, Q.
CMR: tứ giác MNPQ là tứ giác có tổng các góc đối diện bù nhau
HELP ME, PLEASE !!!!!!!!!!!!!!!!!!!!!
2. Cho tứ giác ABCD có phân giác trong các góc A và B cắt nhau tại M, phân giác trong các góc C và D cắt nhau tại P. Hai đoạn thẳng AM và DP cắt nhau tại Q, hai đoạn thẳng BM và CP cắt nhau tại N. Chứng minh rằng tứ giác MNPQ có các góc đối bù nhau.3. Cho tứ giác ABCD có . Hai tia BA, CD cắt nhau tại E, hai tia BC, AD cắt nhau tại F. Phân giác trong các góc cắt nhau tại I. Cmr: .4. Cho tứ giác ABCD . Hai tia BA, CD cắt nhau tại E, hai tia BC, AD cắt nhau tại F. Phân giác trong các góc cắt nha...
Đọc tiếp
2. Cho tứ giác ABCD có phân giác trong các góc A và B cắt nhau tại M, phân giác trong các góc C và D cắt nhau tại P. Hai đoạn thẳng AM và DP cắt nhau tại Q, hai đoạn thẳng BM và CP cắt nhau tại N. Chứng minh rằng tứ giác MNPQ có các góc đối bù nhau.
3. Cho tứ giác ABCD có 
. Hai tia BA, CD cắt nhau tại E, hai tia BC, AD cắt nhau tại F. Phân giác trong các góc 
cắt nhau tại I. Cmr: 
.
4. Cho tứ giác ABCD . Hai tia BA, CD cắt nhau tại E, hai tia BC, AD cắt nhau tại F. Phân giác trong các góc cắt nhau tại I. Cmr: 
.
5. Cho tứ giác ABCD có , 
. Trên tia đối của tia DA lấy điểm E sao cho 
. Cmr:
a) 
.
b) AC là phân giác trong góc 
.
cho tứ giác ABCD, các phân giác trong của các góc A, B, C,D cắt tại M, N, P, Q.
CM: Tứ giác MNPQ có tổng các góc đối diện bù nhau
Các đường phân giác trong của tứ giác ABCD cắt nhau tạo thành tứ giác MNPQ. Chứng minh rằng tứ giác đó có các góc đối bù nhau
Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Các đường phân giác trong của tứ giác ABCD cắt nhau tạo thành tứ giác MNPQ. Chứng minh rằng tứ giác đó có các góc đối bù nhau
Có: góc a1+b1= 180-apb
góc c1+d1= 180-cmd
từ 2 cái suy ra a1+b1+c1+d1=360-tổng 2 góc đối(gọi tắt là T2GD nha)
suy ra 360-360/2=T2GD (vì a1=1 nửa góc a, tương tự các cái kia suy ra tổng abcd1 bằng 360/2, tổng các góc trong tg=360)
suy ra 2 góc đối bù nhau
cmtt suy ra 2 góc đối kia cũng bù nhau
Đúng 0
Bình luận (0)
cho tứ giác abcd các tia phân giác của các góc a b c d cắt nhau tạo thành 1 tứ giác . chứng minh tứ giác nhận được có các góc đối bù nhau
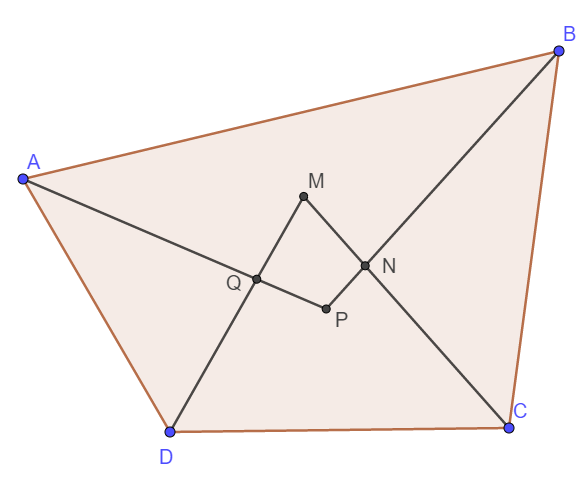
Gọi giao điểm các đường phân giác trong tứ giác ABCD lần lượt là M, N, P, Q như hình vẽ bên trên.
Xét tam giác APB có: \(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=\frac{360^o-\widehat{DAB}-\widehat{CBA}}{2}\)
Tương tự xét tam giác MCD ta cũng có:
\(\widehat{DMC}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}\)
Suy ra \(\widehat{QMN}+\widehat{QPN}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}+\frac{360^o-\widehat{DAB}-\widehat{ABC}}{2}\)
\(=\frac{720^o-360^o}{2}=180^o\)
Do tổng 4 góc trong một tứ giác bằng 360o nên ta cũng có \(\widehat{MQP}+\widehat{MNP}=360^o-180^o=180^o\)
Vậy tứ giác MNPQ có các góc đối bù nhau.
Đúng 2
Bình luận (0)
cho tứ giác abcd các tia phân giác của các góc a b c d cắt nhau tạo thành 1 tứ giác . chứng minh tứ giác nhận được có các góc đối bù nhau
cho tứ giác ABCD , đường p/giác góc A,B,C,D đường này cắt đường kia tại M,N,P,Q.
CMR tứ giác MNPQ là tứ giác có tổng các góc đối diện bằng nhau