giúp em với ak em cần gấp 😓

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, đường cao BH. Chứng minh rằng BAC=2CBH.
(mọi người giúp em với ak. Cần gấp😓😥😢)
Sửa đề:
Cho tam giác ABC cân tại A, đường cao BH. Chứng minh
rằng \(\widehat{BAC}=\widehat{CBH}\).
Bạn xem lại đề nhé!
Đúng 0
Bình luận (1)
Ta có : \(\widehat{BAC}=180^0-2\widehat{ACB}\) (vì góc ABC = góc ACB do tam giác ABC cân tại A)
Do đó: \(\widehat{BAC}=2\left(90^0-\widehat{ACB}\right)=2\widehat{CBH}\) (đpcm)
Đúng 0
Bình luận (1)
Qua văn bản cuộc chia tay của những con búp bê,Em hãy viết một đoạn văn ngắn(khoảng 10dòng)nêu cảm nhận của em về vai trò của gia đình Giúp em với ạ,em đang cần gấp ạ😓
Giúp mình câu 3 với ạ. Cần gấp 😓😓😓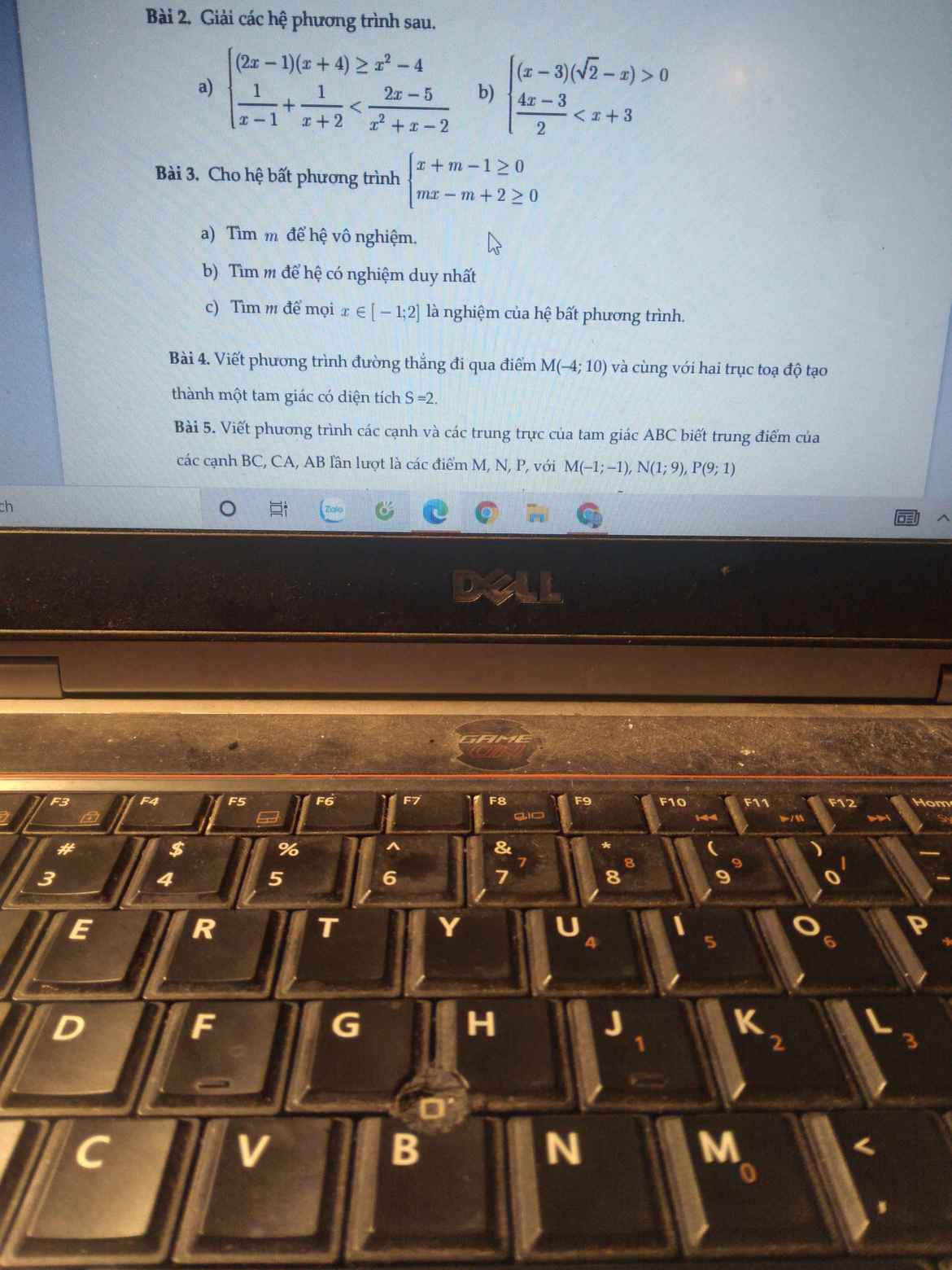
C3: Hệ bpt trở thành: \(\left\{{}\begin{matrix}x\ge1-m\\mx\ge2-m\end{matrix}\right.\)
a, Để hệ phương trình vô nghiệm thì \(m=0\)
b, Để hệ có nghiệm duy nhất thì \(\left\{{}\begin{matrix}m\ne0\\\dfrac{m-2}{m}=1-m\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}m\ne0\\m=\pm\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(m=\pm\sqrt{2}\)
c, \(x\in\left[-1;2\right]\) \(\Leftrightarrow\) \(-1\le x\le2\)
Để mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt trên thì
\(\left\{{}\begin{matrix}-1\le1-m\le2\\-1\le\dfrac{2-m}{m}\le2\end{matrix}\right.\) với \(m\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}2\ge m\ge-1\\m\ge\dfrac{2}{3}\end{matrix}\right.\) \(\left(m\ne0\right)\)
\(\Leftrightarrow\) \(2\ge m\ge\dfrac{2}{3}\)
Vậy \(m\in\left[\dfrac{2}{3};2\right]\) thì mọi \(x\in\left[-1;2\right]\) là nghiệm của hệ bpt
Chúc bn học tốt!
Đúng 2
Bình luận (0)
Giúp mình với. Mình đang cần gấp ạ😓😓😓

27.
Bán kính mặt cầu ngoại tiếp tứ diện vuông được tính bằng:
\(R=\sqrt{\dfrac{OA^2+OB^2+OC^2}{4}}=\sqrt{\dfrac{1^2+2^2+3^2}{4}}=\dfrac{\sqrt{14}}{2}\)
28.
Từ giả thiết suy ra \(A\left(2;2;2\right)\)
Gọi điểm thuộc mặt Oxz có tọa độ dạng \(D\left(x;0;z\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(x-2;-2;z-2\right)\)
\(\overrightarrow{BD}=\left(x+2;-2;z\right)\) ; \(\overrightarrow{CD}=\left(x-4;-1;z+1\right)\)
D cách đều A, B, C \(\Rightarrow\left\{{}\begin{matrix}AD=BD\\AD=CD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x+2\right)^2+4+z^2\\\left(x-2\right)^2+4+\left(z-2\right)^2=\left(x-4\right)^2+1+\left(z+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+z=1\\2x-3z=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}z=-\dfrac{1}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow P\left(\dfrac{3}{4};0;-\dfrac{1}{2}\right)\)
Đúng 1
Bình luận (0)
29.
Do tâm I mặt cầu thuộc Oz nên tọa độ có dạng: \(I\left(0;0;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(-3;1;z-2\right)\\\overrightarrow{BI}=\left(-1;-1;z+2\right)\end{matrix}\right.\)
Mặt cầu qua A, B nên \(AI=BI\)
\(\Leftrightarrow3^2+1^2+\left(z-2\right)^2=1^2+1^2+\left(z+2\right)^2\)
\(\Leftrightarrow8z=8\Rightarrow z=1\)
\(\Rightarrow I\left(0;0;1\right)\Rightarrow R=IB=\sqrt{1^2+1^1+3^2}=\sqrt{11}\)
Phương trình mặt cầu:
\(x^2+y^2+\left(z-1\right)^2=11\)
Đúng 1
Bình luận (0)
30.
Từ phương trình mặt cầu ta có:
\(R=\sqrt{1^2+\left(-2\right)^2+2^2-\left(-m\right)}=\sqrt{m+9}\)
\(\Rightarrow\sqrt{m+9}=5\Rightarrow m=16\)
31.
Khoảng cách giữa điểm M và điểm đối xứng với nó qua Ox là \(2\sqrt{y_M^2+z_M^2}=2\sqrt{65}\)
32.
Gọi \(I\left(x;y;z\right)\) là tâm mặt cầu
\(\overrightarrow{AI}=\left(x-1;y;z\right)\) ; \(\overrightarrow{BI}=\left(x;y-1;z\right)\) ; \(\overrightarrow{CI}=\left(x;y;z+1\right)\); \(\overrightarrow{DI}=\left(x-1;y;z-3\right)\)
Do I là tâm mặt cầu
\(\Rightarrow\left\{{}\begin{matrix}AI=BI\\AI=CI\\AI=DI\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+y^2+z^2=x^2+\left(y-1\right)^2+z^2\\\left(x-1\right)^2+y^2+z^2=x^2+y^2+\left(z-1\right)^2\\\left(x-1\right)^2+y^2+z^2=\left(x-1\right)^2+y^2+\left(z-3\right)^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-x+y=0\\-x+z=0\\-6z+9=0\end{matrix}\right.\) \(\Rightarrow x=y=z=\dfrac{3}{2}\)
Hay \(I\left(\dfrac{3}{2};\dfrac{3}{2};\dfrac{3}{2}\right)\) \(\Rightarrow D\) đúng
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
mn ơi giúp em với em cần gấp ak
mọi người ơi giúp em với ạ SOS!!!
Đúng 0
Bình luận (0)
Em có nhận xét gì về mối quan hệ giữa thực vật với môi trường ?
Mình đang cần gấp 😓😓😓
là chống lũ lụt ,điều hòa khí hậu,...
CHÚC HỌC TỐT
Giúp em câu b bài 1 với ạ😓😓😓😓😓😓
Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)
Đúng 0
Bình luận (0)
Mn trả lời giúp em với ạk:
Đánh giá ý nghĩa việc sử dụng kim loại đối với mức phát triển kinh tế nước ta ngày nay. E đang cần gấp ạk😓😓😓😓
Công cụ kim khí đã mở ra một thời đại mới mà tác dụng và năng suất lao động của nó vượt xa thời đại đồ đá. Đặc biệt là công cụ bằng sắt thì không có một công cụ đá nào có thể so sánh được. Nhờ có đồ kim khí, nhất là sắt, người ta có thế khai phá những vùng đất đai mà trước kia chưa khai phá nổi, có thể cày sâu cuốc bẫm, có thể xẻ gỗ đón" thuyền đi biển, xẻ đá làm lâu đài và bản thân việc đúc sắt cũng là một ngành sản xuất quan trọng bậc nhất.
Đây thực sự là một cuộc cách mạng trong sản xuất. Lần đầu tiên trên chặng đường dài của lịch sử loài người, con người có thể làm ra một lượng sản phẩm thừa.
![]()
Đúng 0
Bình luận (2)
Giúp em bài 2 với😓😓😓
\(\dfrac{x-3}{3x-5}< \dfrac{3x-5}{x-3}.\left(x\ne3;x\ne\dfrac{5}{3}\right).\)
\(\Leftrightarrow\dfrac{x-3}{3x-5}-\dfrac{3x-5}{x-3}< 0.\Leftrightarrow\dfrac{\left(x-3\right)^2-\left(3x-5\right)^2}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{x^2-6x+9-\left(9x^2-30x+25\right)}{\left(3x-5\right)\left(x-3\right)}< 0.\) \(\Leftrightarrow\dfrac{x^2-6x+9-9x^2+30x-25}{\left(3x-5\right)\left(x-3\right)}< 0.\)
\(\Leftrightarrow\dfrac{-8x^2+24x-16}{\left(3x-5\right)\left(x-3\right)}< 0.\Leftrightarrow\dfrac{8x^2-24x+16}{\left(3x-5\right)\left(x-3\right)}>0.\)
\(\Leftrightarrow\dfrac{8\left(x^2-3x+2\right)}{\left(3x-5\right)\left(x-3\right)}>0.\Leftrightarrow\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}>0.\)
Đặt \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right).\)
Lập bảng xét dấu:
| x | \(-\infty\) 1 \(\dfrac{5}{3}\) 2 3 \(+\infty\) |
| x - 2 | - | - | - 0 + | + |
| x - 1 | - 0 + | + | + | + |
| 3x - 5 | - | - 0 + | + | + |
| x - 3 | - | - | - | - 0 + |
| f (x) | + 0 - || + 0 - || + |
Vậy \(\dfrac{\left(x-2\right)\left(x-1\right)}{\left(3x-5\right)\left(x-3\right)}=f\left(x\right)>0.\) \(\Leftrightarrow x\in\left(-\infty;1\right)\cup\left(\dfrac{5}{3};2\right)\cup\left(3;+\infty\right).\)
Đúng 1
Bình luận (0)
a)
\(\left\{{}\begin{matrix}2x^2+7x-4\ge x^2-4\\\dfrac{2x-1}{x^2+x-2}< \dfrac{2x-5}{x^2+x-2}\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x^2+7\ge0\\\dfrac{2x-5-2x+1}{x^2+x-2}>0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\dfrac{-4}{x^2+x-2}>0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x\left(x+7\right)\ge0\\\left(x-1\right)\left(x+2\right)< 0\end{matrix}\right.\)
ta có x+2>x-1
=>x-1<0 và x+2 >0 để thỏa điều kiện =>x<1 và x>-2(hay -2<x<1)(1)
vì -2<x<1 nên x+7>0
=>x\(\ge\)0 để thỏa điều kiện(2)
từ (1) và (2) =>0\(\le\)x<1
b)
\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\4x-3< 2\left(x+3\right)\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\2x-9< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}\left(x-3\right)\left(\sqrt{2}-x\right)>0\\x< \dfrac{9}{2}\end{matrix}\right.\)
có 2 TH xảy ra để thỏa điều kiện
TH1 (x-3)<0 và (\(\sqrt{2}\)-x)<0=>\(\sqrt{2}\)<x<3(nhận)
TH2 (x-3)>0 và (\(\sqrt{2}\)-x)>0=>3<x<\(\sqrt{2}\)(loại)
em nghĩ như nào làm như v thôi có gì sai chị xem và sửa hộ em nhá ![]()
Đúng 0
Bình luận (0)





















