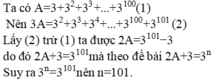Cho A =3+32+33+...+3100.tim so tu nhien N biet :2a +3=3n

Những câu hỏi liên quan
cho A 3+32 +33+....+3100 Tìm số tự nhiên n , biết rằng 2A + 3 3n
Đọc tiếp
cho A =3+32 +33+....+3100
Tìm số tự nhiên n , biết rằng 2A + 3 = 3n![]()
![]()
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
Đúng 0
Bình luận (1)
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
Đúng 1
Bình luận (1)
Cho
A
3
+
3
2
+
3
3
+
.
.
.
+
3
100
. Tìm số tự nhiên n biết rằng 2A+3
3
n
A. n99 B. n100 C. n101 D. n102
Đọc tiếp
Cho A = 3 + 3 2 + 3 3 + . . . + 3 100 . Tìm số tự nhiên n biết rằng 2A+3= 3 n
A. n=99
B. n=100
C. n=101
D. n=102
Cho:
A
3
+
3
2
+
3
3
+
.
.
.
+
3
100
Tìm số tự nhiên n biết rằng: 2A+3
3
n
Đọc tiếp
Cho: A = 3 + 3 2 + 3 3 + . . . + 3 100
Tìm số tự nhiên n biết rằng: 2A+3 = 3 n
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
Đúng 0
Bình luận (0)
cho A = 1+3+3^2+3^3+......+3^10. Tim so tu nhien n biet:2.A+1=3n
\(A=1+3+3^2+3^3+...+3^{10}\)
=>\(3A=3\left(1+3+3^2+3^3+...+3^{10}\right)\)
=>\(3A=3+3^2+3^3+3^4+...+3^{11}\)
=>\(3A-A=\left(3+3^2+3^3+3^4+...+3^{11}\right)-\left(1+3+3^2+3^3+...+3^{10}\right)\)
=>\(2A=3^{11}-1\)
=>\(2A+1=3^{11}\)
=>\(n=3^{11}:3=3^{10}\)
Đúng 0
Bình luận (0)
1,tim 2 so tu nhien biet tong chung = 66 UCLN=6 co 1 so chia het cho 5
2,tim 2 so tu nhien biet hieu chung = 84 UCLN = 12
3,tim 2 so tu nhien biet tich = 864 UCLN=6
4,cho 3n+1 va 5n+4 la 2 so nguyen to cung nhau tim UCLN cua 3n+1 va 5n+4
5,cho a=123456789;b=987654321 . Tim UCLN cua a va b
Solution
We have: 3A = 3. (1 + 3 + 32 + 33 + ... + 399 + 3100) (1 + 3 + 32 + 33 + ... + 399 + 3100)
3A = 3 + 32 + 33 + ... + 3100 + 31013 + 32 + 33 + ... + 3100 + 3101
Inferred: 3A - A = (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100)
2A = 3101−13101−1
⇒⇒ A = 3101−123101−12
So A = 3101−12
Please help me
Dịch ra là: Ta có: 3A = 3. (1 + 3 + 32 + 33 + ... + 399 + 3100) (1 + 3 + 32 + 33 + ... + 399 + 3100) 3A = 3 + 32 + 33 + ... + 3100 + 31013 + 32 + 33 + ... + 3100 + 3101 Suy ra: 3A - A = (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) ⇒⇒ A = 3101−123101−12 Vậy A = 3101−12
Mà đoạn 2A sai nhé bạn, sửa lại:
2A = 3101−13101−1 2A=-10001
A=-10001/2
A=-5000,5
Vậy A=-5000,5
tim so tu nhien n,biet:
3n+13 chia het cho 2n+3(voi n>1)
tim so tu nhien n,biet:
3n+13 chia het cho 2n+3(voi n>1)
cho A=3+32+33+...+32009.tim so tu nhien n biet rang 2A+3=3n
\(3A=3^2+3^3+3^4+...+3^{2010}\)
\(3A-A=\left(3^2+3^3+3^4+..+3^{2010}\right)-\left(3+3^2+3^3+....+3^{2009}\right)\)
\(2A=3^{2010}-3\)(1)
(1) => \(3^{2010}-3+3=3^{2010}\)
=> n = 2010
Đúng 0
Bình luận (0)
A = 3 + 32 + 33 + ... + 32009
3A = 32 + 33 + 34 + ... + 32010
3A - A = (32 + 33 + 34 + ... + 32010) - (3 + 32 + 33 + ... + 32009)
2A = 32010 - 3
3n = 2A + 3
3n = 22010 - 3 + 3
3n = 32010
n = 2010
Đúng 0
Bình luận (0)