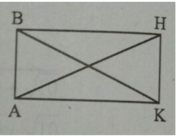
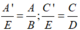Cho 4 điểm thỏa mãn điều kiện : AB//CD ; AD//BC
Gọi P, Q lần lượt là trung điểm của DC và BC. Gọi M là trung điểm AB. Gọi E và F lần lượt là giao điểm của BD với AP và AQ, O là giao điểm của AC và BD
a. CM: O là trung điểmcủa AC và BD
b. C, F, M thẳng hàng
c. DE=EF=AB










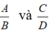 ,ta tìm được hai phân thức cùng mẫu
,ta tìm được hai phân thức cùng mẫu 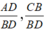 , và thỏa mãn điều kiện :
, và thỏa mãn điều kiện :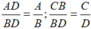 .
.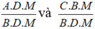 và lần lượt bằng hai phân thức
và lần lượt bằng hai phân thức 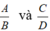 .
.