cho tam giác ABC có góc A =90 độ, đường cao AH. trên tia CB lấy M sao cho CM=CA Đường vông góc với BC tại M cắt AB tại K. So sánh AK và KM

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A Trên tia đối của tia AC lấy điểm K sao cho AK = AC AH Cho AB = 8 cm AC = 6 cm Tính độ dài cạnh BC b Chứng minh BK bằng BC c so sánh hai góc nhọn b và c d kể km vuông góc với BC K M cắt ba tại H chứng minh ch vuông góc với BC CA
Cho tam giác ABC vuông tại A có ABAC. Trên tia đối của tia AC lấy điểm D sao cho ADAB. Trên tia đối của tia AB lấy điểm E sao cho AEAC a. So sánh các góc của tam giác ABC. Chứng minh BDBC b. Chứng minh BCDE, tam giác ABC vuông cân và BC//CE c. Kẻ đường cao AH của tam giác ABC, đường cao AH cắt DE tại M. Từ A kẻ đường vuông góc với CM tại K. đường thẳng này cắt BC tại N. Chứng minh rằng MN//AB
Đọc tiếp
Cho tam giác ABC vuông tại A có AB<AC. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Trên tia đối của tia AB lấy điểm E sao cho AE=AC
a. So sánh các góc của tam giác ABC. Chứng minh BD<BC
b. Chứng minh BC=DE, tam giác ABC vuông cân và BC//CE
c. Kẻ đường cao AH của tam giác ABC, đường cao AH cắt DE tại M. Từ A kẻ đường vuông góc với CM tại K. đường thẳng này cắt BC tại N. Chứng minh rằng MN//AB
1. Cho xx//yy, MN cắt xx tại M, yy tại N. E, F thuộc yy về 2 phía của N : NE NFMN.CMR:a) ME, MF là 2 tia phân giác của góc xMN, xMN b) tam giác MEF vuông2. Cho tam giác ABC cân tại A, trên tia đối của tia BC lấy điểm D ,E sao cho CEBD . Nối AD, AE. So sánh góc ABD với ACE. CM tam giác ADE cân3. CHOtam giác ABC tia phân giác góc B, C cắt nhau tại O. Qua O kẻ đường thẳng song song với BC, cắt AB tại D, cắt AC tại E. CM DE DB +EC4. CHO TAM GIÁC ABC VUÔNG TẠI A và góc B 60°. Cx vuông góc với B...
Đọc tiếp
1. Cho x'x//y'y, MN cắt x'x tại M, y'y tại N. E, F thuộc y'y về 2 phía của N : NE =NF=MN.CMR:a) ME, MF là 2 tia phân giác của góc xMN, x'MN b) tam giác MEF vuông
2. Cho tam giác ABC cân tại A, trên tia đối của tia BC lấy điểm D ,E sao cho CE=BD . Nối AD, AE. So sánh góc ABD với ACE. CM tam giác ADE cân
3. CHOtam giác ABC tia phân giác góc B, C cắt nhau tại O. Qua O kẻ đường thẳng song song với BC, cắt AB tại D, cắt AC tại E. CM DE =DB +EC
4. CHO TAM GIÁC ABC VUÔNG TẠI A và góc B =60°. Cx vuông góc với BC, trên tia Cx lấy đoạn CE=CA ( CE, CA CÙNG PHÍA VỚI BC ). KÉO DÀI CB LẤY F : BF =BA. CM TAM GIÁC ABC ĐỀU VÀ 3 ĐIỂM E, A, F THẲNG HÀNG
5. Cho tam giác ABD : góc B=2D, kẻ AH vuông góc với BD (H thuộc BD ). Trên tia đối của tia BA lấy BE =BH. Đường thẳng EH cắt AD tại F. CM FH=FA =FD
6. Cho tam giác ABC cân tại A, đường cao AH. Trên tia AH lấy điểm D sao cho H là trung điểm của đoạn thẳng AD. Nối CD. CM CD=AB và CB là tia phân giác của góc ACD
7. CHO tam giác ABC cân tại A, đường cao BH. CMR góc BAC =2 CBH
8. Cho tam giác ABC có góc B =60, 2 tia phân giác AD và CE của tam giác cắt nhau tại I. CMR tam giác IDE cân
9. Cho tam giác ABC cân tại A, đường cao AH, HD, HE lần lượt là đường cao của tam giác AHB, AHC. trên tia đối của tia DH, EH lấy điểm M, N: DM=DB, EN =EH.CMR: a) tam giác AMN và tam giác HMN cân b) góc MAN=2BAC
1. Cho tam giác ABC có góc A=90 độ. Đường cao AH. Trên cạnh BC lấy D sao cho BD=BA. Đường vuông góc với BC tại D cắt AC tại E a) So sánh AE và DE
b) CMR : Tia AD là tia phân giác của góc HAC
c) Đường phân giác góc ngoài đỉnh C cắt đường thẳng BC ở K. Tính BAK
d) CMR : AB + AC < BC + AH
e) So sánh HD và DC
a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
a) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)
Cho tam giác ABC vuông ở A Trên tia đối của tia AC lấy điểm K sao cho AK = AC a Cho a b 8 cm AC bằng 6 cm Tính độ dài cạnh BC
B Chứng minh BK bằng BC
C So sánh hai góc nhọn B và C
Kẻ km vuông góc với BC K M cắt BC tại H chứng minh ch vuông góc với BC CA
Mọi người giúp đỡ cho mik nhen, bn nào trả lời câu hỏi của mình sớm nhất, đúng, kb, mik chọn luôn nhen ♡♡
Cho tam giác ABC có C = 90 độ, BC = 3cm, CA = 4cm. Tia phân giác BK( K thuộc CA), kẻ KA vuông góc với AB tại E.
a, Tính AB
b, Chứng minh BC = BE
c, Trên tia đối của tia CB lấy điểm M sao cho CM = AE. Chứng minh E,K,M thẳng hàng. So sánh KM và KE.
d, Chứng minh CE song song với MA
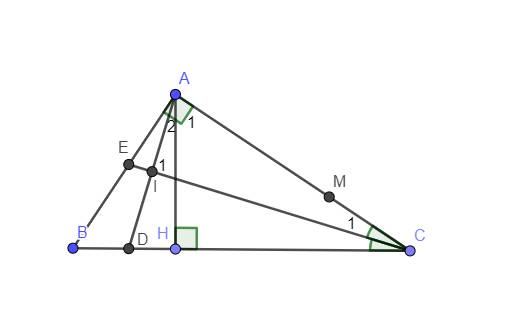
Cho tam giác ABC có góc A = 90 độ. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh góc BAH = góc ACB.
b) Tia phân giác góc BAH và tia phân giác góc ACB cắt nhau tại I. Tính góc AIC
c) Cho AC > AB Trên cạnh AC lấy điểm M sao cho CM= AB. So sánh CM và BH.
`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
Đúng 2
Bình luận (0)
1. Cho tam giác ABC đường phân giác ngoài của góc B và góc C cắt nhau tại K. Chứng minh rằng:a) AK là phân giác góc Ab) Từ K kẻ KM vuông góc với AB, KN vuông góc với AC. So sánh KM và KNc) Vẽ tia phân giác góc ABC cắt KC ở E. Chứng minh AE vuông góc với AK2. Cho tam giác ABC vuông tại A vẽ đường cao AH.a) Chứng minh 3 tam giác ABC, HBA, HAC có 3 góc bằng nhau từng đôi một.b) Tia phân giác góc BAH cắt BC tại D. Chứng minh góc CAD góc CDA từ đó kết luận gì về tam giác CAD.c)Trên tia CA lấy điểm K...
Đọc tiếp
1. Cho tam giác ABC đường phân giác ngoài của góc B và góc C cắt nhau tại K. Chứng minh rằng:
a) AK là phân giác góc A
b) Từ K kẻ KM vuông góc với AB, KN vuông góc với AC. So sánh KM và KN
c) Vẽ tia phân giác góc ABC cắt KC ở E. Chứng minh AE vuông góc với AK
2. Cho tam giác ABC vuông tại A vẽ đường cao AH.
a) Chứng minh 3 tam giác ABC, HBA, HAC có 3 góc bằng nhau từng đôi một.
b) Tia phân giác góc BAH cắt BC tại D. Chứng minh góc CAD= góc CDA từ đó kết luận gì về tam giác CAD.
c)Trên tia CA lấy điểm K sao cho CK=CH. Chứng minh AD song song với HK
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
Đúng 0
Bình luận (0)
cho tam giác ABC có góc B=90 độ và AB<BC, đường cao BH.Trên tia HA lấy điểm D sao cho HD=HC a)c/m BC=BS b)So sánh AH vs HC c)Từ A kẻ đường thẳng vuông góc với BD, cắt BD tại K, cắt BN tại I. C/m BA vuông góc DI d)Tìm điều kiện của tam giác ABC để tam giác DBI là tam giác đều














