Chứng minh tính chất đường phân giác ngoài trong tam giác

Những câu hỏi liên quan
Vẽ hình và chứng minh tính chất đường phân giác trong và ngoài của tam giác.
Cho tam giác ABC, tia phân giác góc BAC cắt tia phân giác góc ngoài tại C của tam giác ABC tại I. Chứng minh ABC=2AIC Gợi ý: Sử dụng tính chất góc ngoài tại đỉnh C của tam giác ABC và giác ngoài tại đỉnh C của tam giác AIC
Chứng minh trong 1 tam giác, đường phân giác trong và 2 đường phân giác ngoài cùng nằm trong một góc thì đồng quy.
Cho tam giác ABC nhọn. Đường phân giác trong AK, đường phân giác ngoài AM ..
a) Chứng minh :Góc MAK=90°
Câu 1: Tam giác ABC có góc A alphaa) Tính góc tạo bởi 2 phân giác trong góc B và góc C.b) Tính góc tạo bởi 2 phân giác ngoài góc B và góc C.c) Tính góc tạo bởi phân giác trong góc B và phân giác ngoài góc C.d) Tính góc tạo bởi phân giác trong góc C và phân giác ngoài góc BCâu 2: Tam giác ABC nhọn, đường cao AH. Gọi M, N là tia đối xứng của H qua AB, AC.a) Tam giác AMB là tam giác gì?b) Chứng minh AM AN AH.c) Gọi giao điểm Mn với AB, AC là F, E. Chứng minh góc AME góc AHK
Đọc tiếp
Câu 1: Tam giác ABC có góc A = \(\alpha\)
a) Tính góc tạo bởi 2 phân giác trong góc B và góc C.
b) Tính góc tạo bởi 2 phân giác ngoài góc B và góc C.
c) Tính góc tạo bởi phân giác trong góc B và phân giác ngoài góc C.
d) Tính góc tạo bởi phân giác trong góc C và phân giác ngoài góc B
Câu 2: Tam giác ABC nhọn, đường cao AH. Gọi M, N là tia đối xứng của H qua AB, AC.
a) Tam giác AMB là tam giác gì?
b) Chứng minh AM = AN = AH.
c) Gọi giao điểm Mn với AB, AC là F, E. Chứng minh góc AME = góc AHK
Cho tam giác ABC. Kẻ AD vuông góc với đường phân giác trong của góc B tại D, kẻ AE vuông góc với đường phân giác ngoài của góc B tại E.
a) Chứng minh tứ giác ADBE là hình chữ nhật.
b) Chứng minh DE//BC
c) Tìm điều kiện của tam giác ABC để tứ giác ADBE là hình vuông.
Cho tam giác ABC. Chứng minh rằng hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.
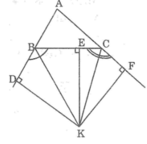
Gọi K là giao điểm của hai tia phân giác của góc ngoài tại đỉnh B và góc ngoài tại đỉnh C.
Kẻ KE ⊥ BC, KF ⊥ AC, KD ⊥ AB
Vì K nằm trên phân giác của ∠(CBD) nên:
KD = KE (tính chất tia phân giác) (1)
Vì K nằm trên tia phân giác của ∠(BCF) nên:
KE = KF (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: KD = KF
Điểm K nằm trong ∠(BAC) cách đều 2 cạnh AB và AC nên K nằm trên tia phân giác của ∠(BAC) .
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M, N lần lượt là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc B; E, F lần lượt là hình chiếu của điểm A trên đường phân giác trong và ngoài của góc C.
a) Chứng minh bốn điểm M, N, E, F thẳng hàng.
b) Tính độ dài cạnh NF theo các cạnh của tam giác ABC.
chứng minh trong 1 tam giác,đường phân giác trong góc trong xuất phát từ mỗi đỉnh và hai đường phân giác ngoài xuất phát từ hai đỉnh kia đồng quy tại 1 điểm
Gọi I là giao của ∠ABC và ∠ACB, gọi D, F, E lần lượt là hình chiếu của I trên
AC, AB, BC
Xét ∆FBI và ∆EBI:
∠FBI=∠IBE(gt)
BI chung
∠BFI=∠IEB=900(gt) =>∆FBI = ∆EBI(g-c-g)
Do đó IF=IE(cạnh tương ứng)
Xét ∆FAI và ∆DAI:
∠FAI=∠IAD(gt)
AI chung
∠AFI=∠IDA=900(gt) =>∆FAI = ∆DAI(g-c-g)
Do đó IF=ID(cạnh tương ứng)
IF=ID;IF=IE =>ID=IE
Xét ∆ECI và ∆DCI:
∠IEC=∠IDC=900(gt)
ID=IE(CMT)
CI chung => ∆ECI = ∆DCI (cạnh huyền -cạnh góc vuông)
Do đó : ∠ECI=∠ICD
=>IC là phân giác góc BCA
Vậy ba đường phân giác trong CI, AI, BI đồng quy tại một diểm












