a)
Ta có

 OA + OB > AB ( Bất đẳng thức tam giác )
 OC + OD > CD ( Bất đẳng thức tam giác )

Công dọc theo vế:

=> OA + OB + OC +OD > AB + CD

=> AC + BD > AB + CD

Bài toán được chứng minh

b)

 Ta có:

 OA + OD > AD ( Bất đẳng thức tam giác )
 OC + OB > CB ( Bất đẳng thức tam giác )

Công dọc theo vế:

=> OA + OD + OC + OB > AD + CB

=> AC + BD > AD + BC

 Bài toán được chứng minh

Chứng minh bất đẳng thức của tam giác 

AC+BC >AB 

Chứng minh bất đẳng thức của tam giác 

AB+BC>AC

AC+BC >AB 

Trên tia đối của tia AB, lấy điểm D sao cho AD = AC (h. 18). Trong tam giác BCD, ta sẽ so sánh BD với BC.
Do tia CA nằm giữa hai tia CB và CD nên
(1) góc BCD > góc ACD
Mặt khác, theo cách dựng, tam giác ACD cân tại A nên
(2) góc ACD = góc ADC = góc BDC
Từ (1) và (2) suy ra :
(3) góc BCD > góc BDC
Trong tam giác BCD, từ (3) suy ra :
AB + AC = BD > BC.
(theo định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác).
Các bất đẳng thức trong kết luận của định lí được gọi là các bất đẳng thức tam giác.

Trên tia đối của tia AB, lấy điểm D sao cho AD = AC (h. 18). Trong tam giác BCD, ta sẽ so sánh BD với BC.
Do tia CA nằm giữa hai tia CB và CD nên
(1)
Mặt khác, theo cách dựng, tam giác ACD cân tại A nên
(2)
Từ (1) và (2) suy ra :
(3)
Trong tam giác BCD, từ (3) suy ra :
AB + AC = BD > BC.
(theo định lí về quan hệ giữa góc và cạnh đối diện trong một tam giác).
Các bất đẳng thức trong kết luận của định lí được gọi là các bất đẳng thức tam giác.

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C

=> HB  + HC = BC

∆AHC vuông tại H => HC < AC

∆AHB vuông tại H => HB < AB

Cộng theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Hay BC < AC + AB

b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC

Do đó AB < BC + AC; AC < BC +AB

(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.

Suy ra H nằm giữa B và C.

⇒ HB + HC = BC

+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)

Lấy (1) + (2) ta được:

HB + HC < AB + AC

Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC

a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông)                                    => AC>HC (1)                                                                                                                                                 Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông)                                        =>AB>HB  (2)                                                                                                                                                 Ta có : HC+HB+BC ( H nằm giũa A và C)  (3)                                                                                                  Từ (1) , (2) và (3) => AC+AB>BC                                                                                                                    b)Xét tam giác ABC có BC là cạnh lớn nhất(gt)                                                                                               =>BC>AB                                                                                                                                                  Ta có : AC>0 => BC+AC>AB                                                                                                                       Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC                                                                             Vì AB>0=>BC+AB>AC

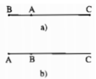
- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.

Trong tam giác ABC ta có AB + AC > BC

- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC

• Nếu A nằm giữa B và C thì AB + AC = BC.

• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.

Suy ra: AC + AB > BC

• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.

Suy ra: AB + AC > BC.

Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C

=> HB + HC = BC

∆AHC vuông tại H => HC < AC

∆AHB vuông tại H => HB < AB

Cộng theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Hay BC < AC + AB

b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC

Do đó AB < BC + AC; AC < BC +AB

(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

bất đẳng thức tam giác sách giáo khoa cx có cách cm đó bạn